L'impulsion de Dirac

[Sarra_sonia]

Bonjour à tous,

On sait que .
Ma question est la suivante:
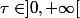
si on prend par exemple un réel , quelle est la valeur exacte de l'intégrale ?

Merci d'avance.

[Doraki]

En maths ta question n'a pas tellement de sens.

L'impulsion de Dirac est une distribution (et pas une fonction), c'est-à-dire un truc qui regarde une fonction Cinfinie à support compact (aussi appelées fonctions tests) φ et qui renvoie φ(0).

Ici on pourrait interpréter ta question comme "que vaut δ appliqué à la fonction indicatrice de [0; τ] ? (ou à celle de R)" sauf que la fonction indicatrice de [0; τ] elle est même pas continue, quant à la fonction indicatrice de R, elle l'est mais elle n'est pas à support compact. Donc on ne peut pas vraiment appliquer δ ni à l'un ni à l'autre.

Ou sinon tu pourrais définir δ comme une sorte de limite de vraies impulsions (c'est-à-dire de fonctions) centrées en 0, symétriques et d'intégrale 1, et dans ce cas son intégrale sur [0; τ] serait 1/2 (parceque t'aurais que la moitié).

Donc bref ça dépend de tes définitions.

[Sarra_sonia]

Je vous remercie pour votre réponse.

Je vais suivre votre deuxième proposition,
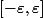
Je prends une suite de classe et à support telle que
et que tend vers lorsque tend vers 0.
Alors
si
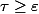
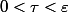
mais dans le cas où son intégrale serait entre 0 et 1/2 !
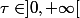
Je cherche une manière pour écrire cette intégrale pour un (à l'aide de la fonction indicatrice par exemple! )

[Doraki]

Ce que je voulais dire c'est que si tu n'as pas une définition de δ ou plutôt de "intégrale de δ(t)* truc(t) dt sur quelquechose", ta question n'a pas de sens et tu perds ton temps.