TF d'une impulsion exponentiel

[nephilim]

Bonjour, dans le cadre d'une études je doit montré étape par étape la TF de la fonction exp(-at) et
a*exp(-at ) mais je doit avouer que je sèche un peu.
Si qqun peu me montré pas a pas comment on arrive au résultat de (2*a)/(a^2+4*pi^2*f^2) pour la 1ere et m'indiquer le départ pour l'autre.
Merci d'avance

[MacManus]

bonjour,

Quelques indications pour arriver au résultat que tu proposes:

1) poser
2) Distinguer 2 cas, avec t0, ce qui revient à décomposer le calcul de la TF avec , puis avec

On suppose que

[nephilim]

Merci de ces indication MacManus . Cela signifie que l'on prend la valeur absolue de t dans la résolution ?
Mon souci est plus sur la résolution de l'intégrale en elle même.
Si je la pose cela donne : exp(-at ). exp(2*j*pi*f*t) de 0 a infini puis de - infini a 0.
Comment dois je faire ? Je fait par parti ? Je remplace les exp par des cos et des sin ?
Honnêtement je ne sais pas comment partir et comment arrivé a déterminer ces TF

[MacManus]

On considère

f est intégrable sur R, donc sur et

Sur , on obtient (sous l'intégrale):
Sur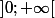 , on obtient (sous l'intégrale):

Tu intègres ces deux expressions (en gardant les exponentielles) avec les bornes correspondantes:


(j'utilise la formulation classique de la transformée de Fourier pour les fonctions intégrables)

[MacManus]

Mon deuxième post concerne le calcul pour aboutir au résultat que tu as énoncé.

En ce qui concerne le calcul de la TF pour f(t)=exp(-at), alors oui, tu pars de :

=...

[nephilim]

Merci pour tous. J'avais oublier que la fonction n'est pas définit sur 0. Je comprend mieux maintenant.
Je ferai le détail du calcule ce soir et verai si j'arrive au bout.
Pour la deuxième le fait de rajouter une constant a devant ne change rien ? La constante passe devant l'intégration c ça ?
Encore merci

[MacManus]

Merci pour tous. J'avais oublier que la fonction n'est pas définit sur 0. Je comprend mieux maintenant.
Je ferai le détail du calcule ce soir et verai si j'arrive au bout.

exp(0)=1

Pour la deuxième le fait de rajouter une constant a devant ne change rien ? La constante passe devant l'intégration c ça ?

C'est ça!

[nephilim]

Ok impeccable.
J'ai trouvé un truc sur le net avec une histoire de parité et en remplaçant l'exp par cos + i sin. Soit disant le i sin s'annule et après il faut faire une double intégration par partie.
Je posterai ça se soir tu me dira ce que tu en pense si tu peu. Merci

[nephilim]

Comment tu fait pour faire les formule de math en direct ?

sinon voila ce que jai trouver

[MacManus]

Comment tu fait pour faire les formule de math en direct ?

Pour voir comment j'ai fait, tu peux cliquer sur un de mes messages en faisant "répondre" et regarder les formules.

Exemple:
[ tex]TF(f) = \int_{\mathbb{R}}f(t)e^{-j2\pi f t}dt [/tex] donne :

les balises en rouges sont indispensables (il ne faut pas mettre un espace entre le "crochet" et le mot "tex" dans va première balise

[MacManus]

Comment tu fait pour faire les formule de math en direct ?

sinon voila ce que jai trouver

Oui je suis d'accord avec cette méthode. Tu as réussi à faire des calculs pour la double intégration par parties ?

[nephilim]

non j'ai rien fait pour le double intégration par partie. j'essaie déjà avec ta méthode.

Je te poste le sujet original comme ça tu comprendra toute l’étude qui a pour finalité la synthèse de filtre numérique.

1) Soit un montage un filtre RC sortie sur C
avec et

On mettra H(f) sous la forme ou est une constante a determiner en fonction de R et C

Jusque la pas de problème

2) Déterminez la transformé de fourrier de la fonction u(t) étant la fonction unité (je pense que tu connait)
En déduire la réponse impulsionnelle du filtre.
Déjà u(t) limite l’intégrale a

après il y aura échantillonnage de la réponse impulsionnelle, Transformé en Z, synthèse d'un FIR et produit de convolution . . . tout un programme et je bloque sur une bête intégrale lol

pour le moment je par sur ce que tu me donnée


Je vais déterminé la primitive, calculé l’intégrale sur l’intervalle et voir si j'arrive au même résultat que donnée.

Par contre sur l'image que j'ai posté avec l'histoire du pair et du cos, je ne comprend pas le 2 devant l'intégrale. si tu peu m’éclairer.

[MacManus]

Pour la transformée tu es bien parti. tu peux considérer l'expression comme une constante. C'est donc facile de trouver une primitive pour l'exponentielle.

Par contre, tu ne trouveras pas le même résultat que sur l'image que tu as mise, puisque tu considères l'expression et non l'expression , ce n'est pas la même chose !!

[MacManus]

Par contre sur l'image que j'ai posté avec l'histoire du pair et du cos, je ne comprend pas le 2 devant l'intégrale. si tu peu m’éclairer.

Et bien il s'agit d'une propriété pour les fonctions paires.
Si f est une fonction réelle, paire, définie et continue sur un intervalle de R, disons [-a,a] pour tout a dans R, alors:
et donc
Tu remarqueras que l'intervalle [-a,a] est symétrique par rapport à 0. Il en est de même pour R.
Si tu intègres une fonction impaire sur un intervalle symétrique par rapport à 0, alors son intégrale est nulle.