Images d'ensembles par homographie

[azboul]

Bonjour à tous,
Voilà je dois trouver les images d'ensembles par l'homographie suivantes (dans le plan complexe) :

h(z) = (z+i)/(z-1).

Voici un des ensembles en question : E={z | Im(z)<1}.

Bon je sais qu'il s'agit des z qui sont dans le cercle trigo, donc j'ai essayer de remplacer z dans h(z) par exp(i;)) puis par a+ib (pour voir ce que ça donnait..) mais ça n'a rien donner...
En fait si on pouvait me donner deux trois pistes ça serais sympa merci.

[fahr451]

bonjour

tu es sûr de ton énoncé ? z= 1 n 'a pas d 'image et est dans D

[azboul]

quel boulet..
En fait ce n'est pas Im(z) mais |z]...

[mathelot]

bonjour,
je n'ai pas la réponse complète mais:

l'ensemble de départ est le disque unité ouvert.
le translate de -
ensuite il y a l'inversion qui le transforme en un domaine non borné.
puis la multiplication par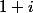 qui est une homothétie de centre l'origine,
de rapport suivie d'une rotation de centre l'origine et d'angle
et on termine par une translation de

je me demande sur quoi l'inversion
transforme le domaine ?

[mathelot]

je répond à ma question:
vers quoi le domaine est transformé par l'inversion
?
de l'égalité:
si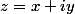 et

d'où
et
La définition du domaine équivaut à:

en exprimant tout ça avec f(z):

d'où:


Je viens donc de montrer que l'image du disque de centre (-1;0) , par l'inversion f, est le demi-plan
d'équation

conclusion:
l'image que tu cherches, par l'application h, est le demi plan inférieur délimité par une droite
de direction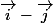 , la frontière étant à une distance
de l'origine.

[azboul]

Ok merci beaucoup pour ton raisonnement il va bien me servir pour la suite de l'exos.
:++: