Hyperplans
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 09 Oct 2015, 22:06
par ilikoko123 » 09 Oct 2015, 22:06
Soient (H1, H2, . . . , Hp) un systeme dhyperplans de lespace
E supposé de dimension finie. Prouver lexistence dun hyperplan H tel que
dim H

Hi < dim H pour tout i

{1, . . . , p}
je me bloque :triste: une piste svp
-
Robot
 par Robot » 09 Oct 2015, 22:10
par Robot » 09 Oct 2015, 22:10
Il vaut mieux supposer pour cet exercice que le corps de base n'est pas fini !
Il suffit alors de prendre H différent de
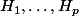
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 09 Oct 2015, 22:18
par ilikoko123 » 09 Oct 2015, 22:18
c'est justement ce que je pensait à faire , qu'est ce qui ns permet de dire qu'il y a un différent des autres ?
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 09 Oct 2015, 22:29
par ilikoko123 » 09 Oct 2015, 22:29
Robot a écrit:Il vaut mieux supposer pour cet exercice que le corps de base n'est pas fini !
Il suffit alors de prendre H différent de
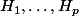
de quel corps vous parlez exactement :hein: ?
ah je comprends
il y a une bijection entre l'ensemble des supplémentaires d'une droite vectorielle donnée et K^n-1 qui est eventuellement un corps infini
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités