Hyperplan, stabilité, dualité

[issoram]

Bonsoir,

Je me permets de vous soumettre une question qui me laisse perplexe:
On considère:
- E un K e.v.
- f un endomorphisme de L(E)
-tf l'application transposée de f définie de E*->E* par tf(g)=g°f

Montrer que si f laisse stable un hyperplan H de E, alors tf laisse stable tous ses supplémentaires K.x0 ou x0 est un élément de E tel que E = H + K.x0 (somme directe).

Je bloque dès le début car pour moi, tf définie de E*->E* ne peut laisser stable un supplémentaire de H (qui appartient à E) alors que définie sur E*??

[GaBuZoMeu]

Bonsoir,

Tu as raison, cet énoncé n'a aucune sens. D'où sort-il ?

[issoram]

Bonsoir,

Il s'agit d'un DM de Spé que j'ai trouvé sur le site d'un professeur de classe prépa.
Dans la première partie, il s'agissait de démontrer des résultats classiques sur l'application transposée.
Je vous poste la deuxième partie complète (la 1ere question étant celle que j'ai évoquée dans mon post initial):

Lemme de Schur : Tout endomorphisme en dimension finie qui laisse stable tout hyperplan est une
homothétie.
1. Montrer que si f laisse stable un hyperplan H, alors tf laisse stable tous ses supplémentaires
K:x0 où x0 appartient à E tel que E = H + K.x0 (somme directe)
2. Montrer que si (x; f (x)) est liée pour tout x de E, alors f est une homothétie.
3. Montrer qu’un endomorphisme qui laisse stable toutes les droites est forcément une homothétie.
4. En déduire le lemme de Schur.

[GaBuZoMeu]

Ce qui est vrai : si un sous-espace F est stable par f, alors son orthogonal pour la dualité est stable par la transposée de f.
En dimension finie, l'orthogonalité fournit une bijection entre hyperplans vectoriels de E et droites vectorielles du dual E*.

[issoram]

Oui, dans la première partie, il était demandé de démontrer l'équivalence entre la stabilité par f d'une partie de E et la stabilité par tf de l'orthogonal de E.
Concernant la bijection entre hyperplans de E et droites de E*, à mon avis c'est la clef de l'exercice... Mais je n'avance pas beaucoup...

[GaBuZoMeu]

Ben, l'orthogonal d'un hyperplan de E, c'est quoi ? Et l'orthogonal d'une droite vectorielle de E*, c'est quoi ?

[issoram]

L'orthogonal d'un hyperplan de E est une droite de E* et réciproquement, aucun souci là dessus.

Je pense avoir une solution mais en reformulant la question 1. en : "Montrer que si f laisse stable un hyperplan de E alors tf laisse stable les droites vectorielles de E de la forme alpha.phi0 où phi0 appartient à E* et alpha appartient à K*
Question 2. ok
Question 3. découle de 2.
Question 4.
Si f laisse stable tout hyperplan de E alors (d'après 1.) tf laisse stable toute droite de E*. D'après 3. tf est une homothétie.
Ensuite on montre que phi: f->tf est injective
puis que: tf=lambda.IdE* = t(lambda.IdE) d'où f= lambda.IdE

[GaBuZoMeu]

Ça serait plutôt, comme je l'indiquais : si f laisse stable un hyperplan, alors la transposée de f laisse stable sa droite orthogonale pour la dualité.
Il faut bien que tu utilises quelque part la bijection canonique entre hyperplans de E et droites de E* pour dire que si f laisse stable tout hyperplan de E, alors sa transposée laisse stable toute droite de E*

[issoram]

Je crois qu'on dit la même chose non?
Par contre il n'y a pas d'isomorphisme "canonique" entre E et E*, car l'isomorphisme en question dépend de la base choisie dans E. (L'isomorphisme est canonique entre E et son bidual E**)

[GaBuZoMeu]

Décidément, tu as l'air d'avoir du mal à lire ce qui est vraiment écrit et tu as tendance à interpréter de travers. Un conseil : lis plus attentivement !
Où vois tu que j'écris qu'il y a un isomorphisme canonique entre E et E* ? J'écris :

la bijection canonique entre hyperplans de E et droites de E*

Cette bijection canonique est donnée par l'orthogonalité pour la dualité. Elle est bien canonique, elle ne dépend d'aucun choix. Et je le répète, c'est cette bijection canonique que tu utilises pour déduire que la transposée de f stabilise toutes les droites vectorielles de E*.

[issoram]

Bonjour GaBuZomeu,

Effectivement j'ai lu votre réponse un peu trop vite et à une heure trop tardive surtout...
Par contre, pour démontrer que laisse stable toute droite de E*, je n'ai pas eu besoin d'invoquer explicitement la bijection entre hyperplans de E et droites de E*:

On considère f un endomorphisme qui laisse stable tout hyperplan H de E.
Soit une droite de 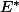, alors est un hyperplan de E et est stable par f.
Pour x et D, on a , puisque et
Ainsi
Ainsi laisse stable toute droite de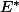

PS: Si vous pouviez éviter le tutoiement... et le ton professoral.... Merci beaucoup

[GaBuZoMeu]

Le tutoiement est l'habitude sur le forum.
Quant au ton professoral, c'est un peu naturel de la part d'un prof. Que veux-tu, j'ai un peu plus de bouteille que toi !

Tu ne parles peut-être pas de bijection, mais tu utilises que toute droite de E* est l'orthogonal d'un hyperplan de E et que . C'est donc un peu jouer sur les mots.
En tout cas, ce que tu écris maintenant est nettement mieux que
"Montrer que si f laisse stable un hyperplan de E alors tf laisse stable les droites vectorielles de E de la forme alpha.phi0 où phi0 appartient à E* et alpha appartient à K*