Groupes des quaternions

[Trident]

Salut, je bloque sur la correction de l'exercice qui vise à démontrer que le groupe des quaternions H8:={-1,1,-i,i,-j,j,-k,k} n'est pas un produit direct.

Déjà, qu'est-ce que ça veut dire ? Doit-on montrer que H8 n'est pas égal à un produit semi direct ou que H8 n'est pas isomorphe à un produit semi direct.
J'aurai tendance à dire qu'il faut montrer que H8 n'est pas isomorphe à un produit semi direct. Ensuite, il y a encore deux cas possibles :

-faut il montrer que H8 n'est pas isomorphe à un produit semi direct H x K avec H et K des sous groupes de H8.

-ou alors, il faut montrer que H8 n'est pas isomorphe à un produit semi direct H x K avec H et K deux groupes quelconques?


Sinon la correction de mon exo (pas du tout rigoureuse) commence comme ceci : Supposons que H8 est un produit s-d : H8= N x K (donc c'est un "=" proposé dans la correction).
On précise que N est un sous groupe de H8 et que K est un sous groupe de H8 mais pourquoi????

Puis il est dit que N inter H est réduit au neutre (là aussi, on a juste un théorème qui dit que si G=A x B est un produit s-d, on pourra toujours se ramener à G=A'x B' avec A'=Ax{1_B} et B'={1_A}xB de tel sorte que A' inter B'= {neutre} mais ce n'est pas précisé).

Ensuite, on distingue deux cas , d'abord si N est d'ordre 4, alors H est d'ordre 2 et on a H isomorphe à Z/2Z. Puis il est dit que le seul élément d'ordre 2 dans H8 est -1 qui appartient simultanément à Net H. Mais pourquoi -1 appartient à N ? Et si N n'est pas un sous groupe de H8, "-1 appartient à N" n'a pas trop de sens ?


Et sinon, pourquoi ne dis-ton pas que N inter H ={neutre} est impossible car tout sous groupe de H8 contient simultanément -1 et 1?

Bref, ce n'est vraiment pas clair dans ma tête. Merci d'avance.

[barbu23]

Bonsoir,

Je vais directement passer à la question principale de ton fil :

Définition : ( Produit semi - direct interne de deux sous groupes et d'un groupe : ) :
est produit semi direct interne de et



- est distingué.
-
-

Le groupe des quaternions possède sous groupes :.

Or, l'intersection d'aucun de ses sous groupes, deux à deux, ne se réduit à .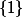
Ce qui contredit l'une des assertions de la définition çi-dessus. :happy3:
Donc, ne peut pas se mettre sous forme d'un produit semi - direct de deux de ses sous groupes.

Cordialement. :happy3:

Edit : Je m'excuse, j'ai mal lu ce que tu veux. :hum: :marteau:

[Trident]

Ok , mais c'est intéressant tout de même.

Je n'ai pas la même définition de ça pour le produit semi direct, j'ai plutôt celle du produit semi direct externe.

Pour H,K des groupes, alpha un morphisme de K dans Aut(H),le produit semi direct de H x K relativement à alpha est le groupe (en prenant soin de le vérifier ! ) dont les éléments sont H x K et la loi est la suivante :

(h,k) * (h',k') = (h*alpha_(k) (h'), kk').

Mais de ce que j'ai pu comprendre, c'est que si un groupe G est isomorphe à un produit semi direct H x K (donc dans ce cas, H et K n'ont aucune raison d'être des sous groupes de G), en notant f l'isomorphisme entre G et HxK, en posant H'=Hx{1}, K'={1}xK et A=f^(-1)(H) et B=f^(-1)(K), on pouvait se ramener à ta définition car alors A et B sont des vrais sous groupes.

Mais alors pourquoi Daniel PERRIN se complique inutilement la tâche dans son cours d'algèbre?

[barbu23]

A mon avis, il faut faire la distinction entre : produit semi-direct interne et produit semi-direct externe.
Le produit semi-direct externe tel que : n'a pas de sens à mon avis, car si c'est le cas, 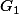d’élément neutre s'injectera dans dans et 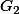d'élément neutre s'injectera dans , donc, finalement va avoir deux éléments neutres distincts, ce qui n'est pas possible à mon avis.
Donc, ne peut pas se mettre sous la forme de produit semi-direct de deux groupes quelconques distincts ( produit semi - direct externe ), mais simplement produit semi direct de sous groupes ( produit semi - direct interne ).

J'espère ne pas avoir dit de bêtises. :happy3:

[Ben314]

Déjà, qu'est-ce que ça veut dire ? Doit-on montrer que H8 n'est pas égal à un produit semi direct ou que H8 n'est pas isomorphe à un produit semi direct.
J'aurai tendance à dire qu'il faut montrer que H8 n'est pas isomorphe à un produit semi direct. Ensuite, il y a encore deux cas possibles :
-faut il montrer que H8 n'est pas isomorphe à un produit semi direct H x K avec H et K des sous groupes de H8.
-ou alors, il faut montrer que H8 n'est pas isomorphe à un produit semi direct H x K avec H et K deux groupes quelconques?

Dans ce genre d'exo, même si c'était écrit "égal", c'est clairement "isomorphe" qu'il faudrait comprendre.
Ensuite, concernant tes deux "cas", ça ne change strictement rien vu que, si un groupe G est isomorphe à un produit semi direct "externe" H x K alors cet isomorphisme te fournit immédiatement deux sous groupes H' et K' de G (images respectives des sous groupes H x{1_K} et {1_H} x K de H x K par l'isomorphisme) tel que G soit égal (et pas isomorphe cette fois) au produit semi direct "interne" H' X K'.

Supposons que H8 est un produit s-d : H8= N x K (donc c'est un "=" proposé dans la correction).
On précise que N est un sous groupe de H8 et que K est un sous groupe de H8 mais pourquoi????

Parce qu'il s'est directement placé dans le cas H' x K' sus mentionné.

Puis il est dit que N inter H est réduit au neutre (là aussi, on a juste un théorème qui dit que si G=A x B est un produit s-d, on pourra toujours se ramener à G=A'x B' avec A'=Ax{1_B} et B'={1_A}xB de tel sorte que A' inter B'= {neutre} mais ce n'est pas précisé).

Si c'est surtout le produit semi direct externe que tu as vu, il faut effectivement voir que dans le produit "externe" H x K l'ensemble H x {1_K} est un sous groupe de H X K isomorphe à H donc on identifie H à cet ensemble et {1_H} x K est un sous groupe de H X K isomorphe à K donc on identifie K avec cet ensemble.

Ensuite, on distingue deux cas , d'abord si N est d'ordre 4, alors H est d'ordre 2 et on a H isomorphe à Z/2Z. Puis il est dit que le seul élément d'ordre 2 dans H8 est -1 qui appartient simultanément à Net H. Mais pourquoi -1 appartient à N ? Et si N n'est pas un sous groupe de H8, "-1 appartient à N" n'a pas trop de sens ?

N est un sous groupe de H8.
-1 est forcément dans N car comme N est de cardinal 4 il doit contenir un x distinct de 1 or un tel x est soit égal à -1, soit de carré égal à -1.

Et sinon, pourquoi ne dis-ton pas que N inter H ={neutre} est impossible car tout sous groupe de H8 contient simultanément -1 et 1?

Je ne sais pas (pourquoi ta correction ne le dit pas) : ça serait effectivement plus simple.
Une explication possible : le prof est un peu arrivé "les mains dans les poches" et il a corrigé "au filling" donc pas forcément avec la méthode la plus simple... ça arrive...

[Trident]

Merci à vous! Ok Ben, c'est bien ce que je pensais dans mon message de 23h09. Le pire c est que Daniel Perrin n'utilise pas cet argument dans son livre et là c'est préparé normalement.