Groupe des quaternions
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 21 Jan 2008, 00:31
par legeniedesalpages » 21 Jan 2008, 00:31
Bonsoir,
je ne comprends pas, le prof nous dit qu'il n'y a pas d'éléments d'ordre 4 dans les groupe des quaternions
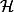
,
Pourtant si je note:
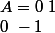)
je trouve
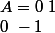)
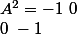)
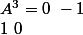)
 = Id)
ce qui veut dire que

est d'ordre 4, non?
merci pour votre aide
 par legeniedesalpages » 21 Jan 2008, 00:45
par legeniedesalpages » 21 Jan 2008, 00:45
Je ne comprends pas, l'article de
http://fr.wikipedia.org/wiki/Groupe_de_quaternions dit qu'il y a trois éléments d'ordre 4 dans ce groupe.
Plus exactement le prof dit que le groupe diédral
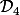
et le groupe quaternionique
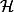
sont tous les deux d'ordre 8, et ne sont pas isomorphes car
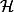
ne possède pas d'éléments d'ordre 4.
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 21 Jan 2008, 08:12
par Dyo » 21 Jan 2008, 08:12
Salut,
je confirme: il y a 3 éléments d'ordre 4 (i,j et k) et les sous-groupes qu'ils
engendrent chacun sont normaux (d'indice 2 dans H).
Dans D4 il n'y a que 2 éléments d'ordre 4 :

et
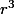
.
 par legeniedesalpages » 21 Jan 2008, 08:15
par legeniedesalpages » 21 Jan 2008, 08:15
Dyo a écrit:Salut,
je confirme: il y a 3 éléments d'ordre 4 (i,j et k) et les sous-groupes qu'ils
engendrent chacun sont normaux (d'indice 2 dans H).
Dans D4 il n'y a que 2 éléments d'ordre 4 :

et
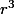
.
Merci Dyo, le prof a du faire une coquille, mais le fait qu'ils n'ont pas autant d'éléments d'ordre 4 font qu'ils ne peuvent être isomorphes, c'est bien ça?
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 21 Jan 2008, 09:38
par Dyo » 21 Jan 2008, 09:38
Ui un isomorphisme conserve les ordres.
(la démonstration est simple)
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 21 Jan 2008, 09:58
par Dyo » 21 Jan 2008, 09:58
Voici une démo (ca devrait être bon :p)
Si

est un isomorphisme et

un élément d'ordre

. Si

est l'ordre de
=y)
.
Je note la loi multiplicativement.
On a
=(f(x))^{d}=f(e)=e)
ca montre que

divise

.
Ca c'est vrai pour tout morphisme, maintenant pour un isomorphisme on a l'égalité. On a:
)^{d_2}=e=f(x^{d_2}))
or
=\{e\})
donc ca implique que
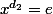
c'est à dire

divise

.
On a donc
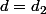
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
et
.