Bonjour à tous,
Je cherche à résoudre l'exercice suivant :
Soit G un groupe agissant proprement, librement et par homéomorphismes sur une variété topologique V. On fixe
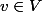
et on note
)
l'image de

dans
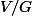
par l'application quotient
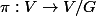
.
1) Soit

un lacet de
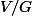
. Expliquer pourquoi il existe un unique chemin
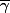
de V tel que
=v)
et
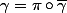
.
On note alors
 \in G)
l'unique élément de

tel que
=\Phi(\gamma)v)
.
2) Montrer que l'application
) \rightarrow G)
,
 = \Phi(\gamma))
est bien définie et que c'est un morphisme de groupes.
3) On suppose V connexe par arcs/ Montrer que

est surjectif.
4) On suppose V simplement connexe. Montrer que

est un isomorphisme.
Voici ce que j'ai fait :
1) Comme G agit proprement, librement et par homéos sur V,

est un revêtement. Il existe donc un unique relèvement
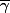
de

tel que
=v \in \pi^{-1}(\{\pi(v)\}))
(théorème vu en cours).
2) Pour montrer que c'est bien défini, je prends deux lacets de V/G

et

basés en
)
homotopes à extrémités fixées (
via une homotopie
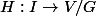
).
D'après un théorème vu en cours, pour tout relèvement
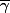
de

, il existe
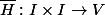
qui relève

et telle que
 = \overline{\gamma}(t), \; \forall t \in I)
.
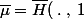)
est un chemin de

qui relève

et
= \overline{\gamma}(0) = v)
(puisque
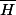
relève

qui est une homotopie à extrémités fixées).
De même,
= \overline{\gamma}(1) = \Phi(\gamma) v)
.
Mais pour montrer que c'est un morphisme de groupes, je bloque ...
Si

et

sont deux lacets de
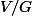
basés en
)
, je prends deux relèvements
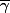
et
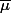
tels que
=v)
et
=\overline{\gamma}(1) \in \pi^{-1}( \{\pi(v)\}))
.
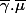
(chemin qui parcourt d'abord
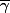
puis
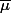
) relève
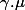
,
 = \overline{\gamma}(0) = v)
et
 = \overline{\mu}(1) = \Phi(\mu)v)
. Et là, problème... vu qu'on aimerait avoir
 = \Phi(\gamma) . \Phi(\mu)v)
.
Alors, je me suis demandé si'il ne fallait pas plutôt prendre
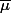
tel que
 = v)
mais, dans ce cas, comment connecter les deux relèvements ???
Merci d'avance pour votre aide !
