Groupe dérivé (licence).
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 29 Mai 2006, 06:51
par Zebulon » 29 Mai 2006, 06:51
Bonjour à tous,
je n'arrive pas à faire cet exercice sur les sous-groupes ditingués. Pouvez-vous m'aider s'il vous plait?
Soit G un groupe. Un
commutateur de G est un élément de la forme

, avec a et b appartenant à G. Soit D(G) le sous-groupe engendré par les commutateurs, appelé le
groupe dérivé.
Montrer que D(G) est distingué et que tout homomorphisme de G dans un groupe abélien se factorise par G/D(G).
Je n'arrive pas à faire la première question et je ne sais plus à quelles conditions un homomorphisme se factorise à travers un sous-groupe distingué...
Merci d'avance!
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 29 Mai 2006, 07:57
par abcd22 » 29 Mai 2006, 07:57
Bonjour !
En fait on peut montrer la propriété plus forte : D(G) est stable par tout automorphisme de G : si

est un automorphisme de G, en notant [a,b] le commutateur

,
 = \varphi(aba^{-1}b^{-1} )=\varphi(a)\varphi(b)\varphi(a^{-1})\varphi(b^{-1}) = \varphi(a)\varphi(b)\varphi(a)^{-1}\varphi(b)^{-1} = [\varphi(a),]\varphi(b)])
, comme les commutateurs engendrent D(G) on a bien
) \subset D(G))
.
Pour pouvoir factoriser à travers un sous-groupe distingué il suffit que ce sous-groupe soit inclus dans le noyau du morphisme.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 29 Mai 2006, 08:02
par Zebulon » 29 Mai 2006, 08:02
abcd22 a écrit:Pour pouvoir factoriser à travers un sous-groupe distingué il suffit que ce sous-groupe soit inclus dans le noyau du morphisme.
Ici, tout commutateur appartient clairement au noyau du morphisme

avec G' abélien.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 30 Mai 2006, 04:52
par Zebulon » 30 Mai 2006, 04:52
J'ai presque oublié de vous remercier! :we:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 30 Mai 2006, 06:43
par Zebulon » 30 Mai 2006, 06:43
abcd22 a écrit:En fait on peut montrer la propriété plus forte : D(G) est stable par tout automorphisme de G :
) \subset D(G))
.
Je ne comprends pas en quoi celà implique que D(G) est un sous-groupe distingué de G. Pouvez-vous m'expliquer s'il vous plaît?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 30 Mai 2006, 07:01
par Zebulon » 30 Mai 2006, 07:01
J'ai peut-une réponse :
On a montré (enfin... VOUS avez montré!) que
)\subseteq{D}(G))
. On veut montré que pour tout
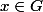
,
=D(G)x)
, ie que pour tout
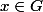
et pour tout
})
,
})
.
Or
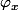
:
\rightarrow{G}\\y\mapsto{xyx^{-1}})
est un automorphime intérieur et on sait que D(G) est stable par automorphisme donc
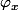
est à valeurs dans D(G) donc pour tout
})
,
})
donc D(G) est distingué dans G.
Est-ce correct?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 30 Mai 2006, 09:47
par yos » 30 Mai 2006, 09:47
Oui c'est correct.
Distingué = invariant (globalement) par automorphisme intérieur.
Et D(G) est invariant par tout automorphisme.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
