Bonjour à tous,
En reprise d’étude, je suis en train de travailler sur les séries, notamment sur les différentes techniques pour tester la convergence ou non d’une série.
La comparaison de suite est souvent utilisée, avec les relations d’équivalence, de négligabilité et de domination. La notion de petit O et d’équivalence est assez claire de mon côté, la notion de grand O est plus floue.
Si je ne dis pas de bétise, U(n) = O (V(n)) signifie que la suite U(n) est dominée par V(n). Dans mon esprit, pour n suffisamment grand, U(n) est inférieure ou égale à V(n) : c’est bien cela ?
Du coup, j’ai du mal à comprendre la définition théorique qui dit : abs(U(n)) <= abs(V(n)) * C
Pouvez-vous m’aider à comprendre cette définition théorique ?
Merci pour votre aide,
François
Grand O
9 messages
- Page 1 sur 1
Re: Grand O
j’ai du mal à comprendre la définition théorique qui dit : abs(U(n)) <= abs(V(n)) * C
La définition théorique ne dit pas ça. Parce que cette phrase est incomplète.
Du coup, c'est normal que tu ne comprennes pas. C'est même heureux que tu ne comprennes pas.
Il manque un mot essentiel dans cette phrase, voire un morceau de phrase tout entier.
Je ne connais pas cette notion de Grand O, donc je ne sais pas quel est le mot qui manque. Mais je pense que la phrase complète, c'est :
Quel que soit le réel C, il existe un rang n à partir duquel abs(U(n)) <= abs(V(n)) * C
Maintenant, la phrase a un sens.
Et maintenant, tu devrais comprendre cette définition théorique.
La définition théorique ne dit pas ça. Parce que cette phrase est incomplète.
Du coup, c'est normal que tu ne comprennes pas. C'est même heureux que tu ne comprennes pas.
Il manque un mot essentiel dans cette phrase, voire un morceau de phrase tout entier.
Je ne connais pas cette notion de Grand O, donc je ne sais pas quel est le mot qui manque. Mais je pense que la phrase complète, c'est :
Quel que soit le réel C, il existe un rang n à partir duquel abs(U(n)) <= abs(V(n)) * C
Maintenant, la phrase a un sens.
Et maintenant, tu devrais comprendre cette définition théorique.
Re: Grand O
Je vais t'apprendre ce qu'il y a de plus efficace comme définition des relations de comparaison:
On dit que un = o ( vn) ssi il existe une suite (an) de limite nulle telle que un=an x vn pour tout n
On dit que un = O (vn) ..............................................................bornée ....................................................................
On dit que un ~ vn ............................................................de limite 1 .......................................................................
On dit que un = o ( vn) ssi il existe une suite (an) de limite nulle telle que un=an x vn pour tout n
On dit que un = O (vn) ..............................................................bornée ....................................................................
On dit que un ~ vn ............................................................de limite 1 .......................................................................
Re: Grand O
J'hésitais, et c'était l'autre option.
En fait, ce qu'il faut retenir de mon message, c'est que quand il manque la moitié de la phrase (les fameux quantificateurs), alors la phrase ne veut plus rien dire.
Et souvent, les gens qui ont des difficultés en maths procèdent ainsi :
- ils lisent une phrase
- ils font l'impasse sur les quantificateurs, ils considèrent que les quantificateurs ne servent à rien.
- ils retiennent donc une phrase incomplète.
- et ils s'étonnent de ne pas comprendre cette phrase incomplète.
En fait, ce qu'il faut retenir de mon message, c'est que quand il manque la moitié de la phrase (les fameux quantificateurs), alors la phrase ne veut plus rien dire.
Et souvent, les gens qui ont des difficultés en maths procèdent ainsi :
- ils lisent une phrase
- ils font l'impasse sur les quantificateurs, ils considèrent que les quantificateurs ne servent à rien.
- ils retiennent donc une phrase incomplète.
- et ils s'étonnent de ne pas comprendre cette phrase incomplète.
Re: Grand O
Merci à vous pour ces explications.
Pour être sûr de bien comprendre, si U(n) = O(V(n)), cela signifie que U(n) ne croit pas plus vite que V(n), c’est bien cela ?
Pour être sûr de bien comprendre, si U(n) = O(V(n)), cela signifie que U(n) ne croit pas plus vite que V(n), c’est bien cela ?
Re: Grand O
Bonsoir,
Plutôt que de chercher une formulation approximative,fais bien l'effort de comprendre la définition qui t'a été donnée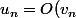) quand il existe une constante
quand il existe une constante 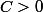 et
et 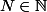 tels que
tels que 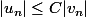 pour tout
pour tout 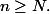 Si
Si  n'est nul pour aucun
n'est nul pour aucun  , ça revient à dire que la suite
, ça revient à dire que la suite ) est bornée. C'est avec cette définition précise que tu pourras travailler, pas avec une idée un peu vague.
est bornée. C'est avec cette définition précise que tu pourras travailler, pas avec une idée un peu vague.
Plutôt que de chercher une formulation approximative,fais bien l'effort de comprendre la définition qui t'a été donnée
Re: Grand O
Pour ce qui est de la compréhension , je suis d'accord avec GaBuZoMeu , mais n'oublies jamais ce que je t'ai dit .
Ça pourra te sauver lors d'une épreuve de concours .
Ça pourra te sauver lors d'une épreuve de concours .
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
