Formule de Taylor

[Otau]

Bonsoir
J'ai cette question toute bête sur la formule de taylor mais je bloque aussi débile que ça puisse paraître.
On a une fonction f De R^n dans R et f(0) = 0 ; f'(0)= 0 et f"(0)= Id
On nous demande de prouver que f(x)= +
En utilisant la formule de Taylor on a bien :

f(0+x) = +
--> f(x) = +
Mais si f"(0)= Id on a ???!!!! Qu'est ce que ça signifie ? Un réel qui vaut un couple ????

Dans la correction on a mais pourquoi on applique Id à x alors que elle est sensée etre bilinéaire.....

[Ben314]

Salut,
Dès le départ, l'énoncé contient la même "boulette" :
1) f(0)=0 : Là O.K. avec le 0 de gauche qui est le 0 de R^n et celui de droite qui est le 0 de R.
2) f'(0)=0 : O.K. aussi,mais différent : le 0 de gauche est toujours le 0 de R^n mais celui de droite est l'application linéaire nulle de R^n dans R.
3) f''(0)=Id : Là, ça ne veut a priori rien dire du tout : f''(0) est une application bilinéaire de R^n x R^n dans R donc ça ne risque absolumnent pas d'être "l'identité" de quoi que ce soit.

[Otau]

Ok merci , je me disais bien qu'il y avait un truc pas net dans cette histoire ^_^

[Ginette4L]

3) f''(0)=Id : Là, ça ne veut a priori rien dire du tout.

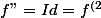C'est une faute de syntaxe vraisemblable: si le développement polynomial d'ordre 2 de . Qu'a-t-on si c'est au voisinage de 0? . Rappelons que la formule de Taylor s'écrit :

[Ben314]

Rappelons que la formule de Taylor s'écrit :

Tu est vraiment sûr que c'est ça la formule de Taylor pour une fonction de R^n dans R ?
Si, par exemple, x et a sont des éléments de R², ça désigne quoi (x-a)² ?

[Ginette4L]

En utilisant la formule de Taylor on a bien :

+

Qui est sensé résoudre l'exo ? J'avais filé la formule de Taylor classique. Ici, il s'agit de Taylor-Young à l'ordre 2.
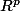
Théorème : Soit une fonction définie sur un ouvert de à valeurs dans et soit un point de cet : .
Si f est k fois différentiable en a, alors : où : . On a celle de Mac Laurin pour la même en : .

[Ginette4L]

Tu est vraiment sure que c'est ça la formule de Taylor pour une fonction de R^n dans R ?
Si, par exemple, x et a sont des éléments de R², ça désigne quoi (x-a)² ?

On a répondu juste avant. Laissons l'intervenant(e) chercher un peu avant de lui mâcher les réponses.