Formule de Taylor
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
celiaJ
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Oct 2011, 18:25
-
par celiaJ » 20 Oct 2012, 14:33
Bonjour,
Je suis en prépa BCPST1 et j'aurais besoin de votre aide pour comprendre la démonstration de la formule de Taylor que je dois savoir refaire pour ma colle ...
Formule à démontrer :
=\bigsum_{k=0}^{n} \frac{P^{(k)}(\alpha)}{k!}(x-\alpha)^k)
Premier cas :
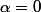
=\bigsum_{k=0}^{n} a_kx^k)
Soit
} = (\bigsum_{k=0}^{n} a_kx^k)^{(j)}= \bigsum_{k=0}^{n} a_k(x^k)^{(j)})
} = \bigsum_{j=0}^{n} a_k(x^k)^{(j)} = \bigsum_{k=j}^{n} \frac{k!}{(k-j)!}a_kx^{k-j})
Ici je n'ai pas compris comment on passe à la dernière égalité.
On fait
. Si
et
D'où il ne reste que le terme pour k=j.
} (0)=a_j\times \frac{j!}{(j-j)!}\times 1=a_j\times j!)
Donc
}(0)}{j!}\times x^k)
On a bien Taylor en 0.
Second cas :
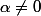
On pose
=P(x+\alpha))
}(x)=P^{(k)}(x+\alpha))
=\bigsum_{k=0}^{n} \frac{Q^{(k)}(0)}{k!}x^k=\bigsum_{k=0}^{n}\frac{P^{(k)}(\alpha)}{k!}x^k)
=P(x -\alpha +\alpha) = Q(x-\alpha))
=\bigsum_{k=0}^{n}\frac{P^{(k)}(\alpha)}{k!}(x- \alpha)^k)
La fin je n'ai pas très bien compris.
Merci d'avance à ceux qui m'aideront =)
-
Alannaria
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Sep 2012, 08:20
-
par Alannaria » 20 Oct 2012, 15:42
D'abord, cet exercice n'a rien à faire dans "La vie en Prépa" mais doit être publié dans le "supérieur".
Après, pour le premier cas, à part une légère coquille en avant-dernière position, c'est la dérivée d'ordre j d'un polynôme que l'on peut aussi redémontrer grâce à une récurrence sur son ordre de dérivation.
Pour le deuxième cas, qu'est ce qui chiffonne au juste car la succession des étapes coule de source?
-
celiaJ
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Oct 2011, 18:25
-
par celiaJ » 20 Oct 2012, 15:46
Alannaria a écrit:D'abord, cet exercice n'a rien à faire dans "La vie en Prépa" mais doit être publié dans le "supérieur".
Après, pour le premier cas, à part une légère coquille en avant-dernière position, c'est la dérivée d'ordre j d'un polynôme que l'on peut aussi redémontrer grâce à une récurrence sur son ordre de dérivation.
Pour le deuxième cas, qu'est ce qui chiffonne au juste car la succession des étapes coule de source?
J'ai finalement compris le second cas. De quelle erreur parlez-vous ?
-
Alannaria
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Sep 2012, 08:20
-
par Alannaria » 20 Oct 2012, 15:50
celiaJ a écrit:J'ai finalement compris le second cas. De quelle erreur parlez-vous ?
L'avant-dernière position: le k a été simplement substitué par un j en indice sans explications attendues.
P.S : commence par poster ce sujet dans la bonne rubrique comme précisé dans le message précédent.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
