Bonjour,
Je cherche une formule explicite donnant la dérivée k-ième de la j-ième puissance
d'une fonction f(x) (infiniment différentiable) sous la forme :
d^k [ f(x)^j ] / dx^k = Somme sur ??? de A_? multiplier par le produit des f(x)^(m_i)
où 0 <= m_1 < m_2 < m_3 < ... < m_p avec m_1+m_2+...+m_p=k.
Que valent ???, A_? et p ?
Toute suggestion et/ou référence sera la bien venue.
Merci,
Zep
Formule multinôme pour derivées
14 messages
- Page 1 sur 1
Re: Formule multinôme pour derivées
Bonjour
En fait ce que vous voulez c'est une formulation détaillée de^{\left[k\right]})
la dérivée k -ième de la fonction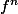 dont on suppose ici qu'elle est au moins k -ième fois dérivable
dont on suppose ici qu'elle est au moins k -ième fois dérivable
c'est ça ou j'ai rien compris?
En fait ce que vous voulez c'est une formulation détaillée de
la dérivée k -ième de la fonction
c'est ça ou j'ai rien compris?
Re: Formule multinôme pour derivées
Vous avez bien compris, mais je cherche plus, à savoir les dérivées doivent être ordonnées par ordre croissant.
J'ai trouvé dans la littérature une formule, à partir de formule multinomiale, mais sans ordre des dérivées.
J'ai trouvé dans la littérature une formule, à partir de formule multinomiale, mais sans ordre des dérivées.
Re: Formule multinôme pour derivées
bah j'ai pas fait grand chose
il faut trouver une formulation générale mais là j'en suis là (mais on peut la trouver en continuant)
^{\left[0\right]}=f^n)
^{\left[1\right]}=nf^{n-1}f^{\left[1\right]})
^{\left[2\right]}=nf^{n-1}f^{\left[2\right]}+n\left(n-1\right)f^{n-2}\left(f^{\left[1\right]}\right)^2)
^{\left[3\right]}=nf^{n-1}f^{\left[3\right]}+n\left(n-1\right)\left(n-2\right)f^{n-3}\left(f^{\left[1\right]}\right)^3+3n\left(n-1\right)f^{n-2}f^{\left[1\right]}f^{\left[2\right]})
il faut trouver une formulation générale mais là j'en suis là (mais on peut la trouver en continuant)
Re: Formule multinôme pour derivées
Ça j'y étais arrivé tout seul 
Ce que je cherche c'est la formule générale.
Merci de la réponse.

Ce que je cherche c'est la formule générale.
Merci de la réponse.
Re: Formule multinôme pour derivées
Bonjour
vous êtes allé jusqu'à où?
à mon avis je pense qu'on va voir se dessiner une formulation générale facile à voir aux alentour de 10
mais là en ayant commencé il y a une demie heure j'en suis qu'à 3
vous êtes allé jusqu'à où?
à mon avis je pense qu'on va voir se dessiner une formulation générale facile à voir aux alentour de 10
mais là en ayant commencé il y a une demie heure j'en suis qu'à 3
Re: Formule multinôme pour derivées
azf a écrit:à mon avis je pense qu'on va voir se dessiner une formulation générale facile à voir aux alentour de 10
eh bien j'ai dit une connerie
C'est ni la première que j'ai dit, ni la dernière que je dirai évidemment
c'est pas une bonne méthode car ça se complique grave
J'ai donc essayé une autre méthode que je ne détaille pas car c'est un vrai merdier
Bon après le calcul est chiant mais on peut écrire un algorithme pas compliqué
Vous avez demandé une formulation générale et ça en est une
Modifié en dernier par azf le 11 Fév 2022, 03:39, modifié 2 fois.
Re: Formule multinôme pour derivées
À partir de là on doit pouvoir arriver à une autre formulation générale plus adéquate car utiliser ça pour un développement en série de Taylor c'est pas top
Re: Formule multinôme pour derivées
Il y avait une coquille dans la formulation générale (j'ai édité pour qu'elle soit conforme)
En voulant la développer j'ai vu que ça clochait
De toute façon pour ce qu'il a demandé il faut la développer
En voulant la développer j'ai vu que ça clochait
De toute façon pour ce qu'il a demandé il faut la développer
Re: Formule multinôme pour derivées
faut que je recommence tout .... je crois que je me suis trompé dans la formulation générale que j'ai écrit plus haut
bon je vais le refaire ...je me suis emmêlé les pinceaux avec le n de l'exposant et le k de la dérivée successive
bon je vais le refaire ...je me suis emmêlé les pinceaux avec le n de l'exposant et le k de la dérivée successive
Re: Formule multinôme pour derivées
bon je l'ai refait (je viens de corriger la formulation générale)
À présent il reste à le développer mais bon c'est plus facile de développer ça à partir du moment où on a la formulation générale du "machin"
À présent il reste à le développer mais bon c'est plus facile de développer ça à partir du moment où on a la formulation générale du "machin"
Re: Formule multinôme pour derivées
Bonjour,
Tu veux une expression du genre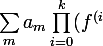})^{m(i)}) indexée par les
indexée par les 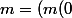,\ldots,m(k))) tels que
tels que 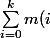=j) et
et 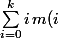= k) ?
?
Tu veux une expression du genre
Re: Formule multinôme pour derivées
Bonjour GaBuZoMeu
Je ne pense pas qu'il te réponde car il est parti (ce fil date d'il y a dix jours) mais ça doit être ce qu'il veut
Je vais essayer de développer la formulation générale donnée plus haut car en tout cas dans cette forme-là c'est clair qu'il n'en veut pas
Je ne pense pas qu'il te réponde car il est parti (ce fil date d'il y a dix jours) mais ça doit être ce qu'il veut
Je vais essayer de développer la formulation générale donnée plus haut car en tout cas dans cette forme-là c'est clair qu'il n'en veut pas
Re: Formule multinôme pour derivées
Alors à partir de la généralisation précédente
^{\left[k\right]}=\displaystyle \sum _{u_{0}=0}^k \binom {k}{u_0} f^{\left[k-u_0\right]}\times)
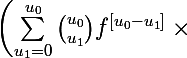
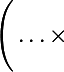
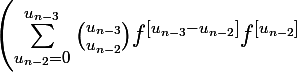\ldots \left.\Bigg)\left.\Bigg))
en la développant j'obtiens quelque chose de plus pratique (à voir si c'est exactement ce que veut mais il est parti)
^{\left[k\right]}=\displaystyle \sum _{u_{0}=0\sim k,u_{1}=0\sim u_{0},\ldots ,u_{n-2}=0\sim u_{n-3}}\binom {k}{u_{0}}\times \binom {u_{0}}{u_{1}}\times \ldots \times \binom {u_{n-3}}{u_{n-2}}\times)

On peut remarquer que par exemple cette écriture là se calcule plus facilement
^{\left[2\right]}=4f^{3}f^{\left[2\right]}+12f^{2}\left(f^{\left[1\right]}\right)^2=)
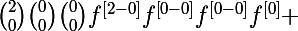
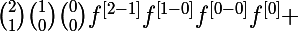
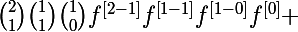
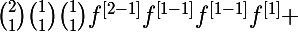
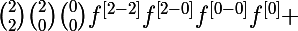
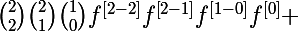
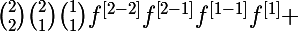
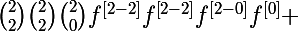
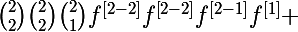
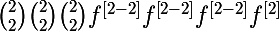
en la développant j'obtiens quelque chose de plus pratique (à voir si c'est exactement ce que veut mais il est parti)
On peut remarquer que par exemple cette écriture là se calcule plus facilement
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
