Bonjour,
j'ai un exercice où l'on me demande de développer la dérivér n ieme de(x^n(1-x)^n)) en utilisant la formule de Leibniz puis de calculer le coefficient devant x^n dans cette dérivée. Et enfin en déduire La somme des k parmis n au carré allant de 0 à n...
Si vous pouviez m'éclairer un peu, car je ne sais pas trop comment utiliser la formule de Leibniz.
Merci d'avance.
Formule de Leibniz
6 messages
- Page 1 sur 1
par Ben314 » 10 Déc 2009, 22:11
Bonsoir,
La formule de Leibniz donne la dérivée n-ième du produit de deux fonctions :
^{(n)}=\bigsum_{k=0}^n\left(\matrix{n\cr k}\right)f^{(k)}g^{(n-k)})
On te demande simplement de l'appliquer aux fonctions
et ^n)
.
La formule de Leibniz donne la dérivée n-ième du produit de deux fonctions :
On te demande simplement de l'appliquer aux fonctions
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par matcail » 10 Déc 2009, 22:52
Ba le problème, c'est que je ne vois pas comment arriver à calculer le coefficient devant x^n comme demandé.
ps : il faut faire la dérivée n ième du produit de x^n et (1-x)^n
ps : il faut faire la dérivée n ième du produit de x^n et (1-x)^n
par Ben314 » 10 Déc 2009, 22:57
1) tu applique (comme on te le demande) la formule de leibnitz => tu obtient une somme.
2) pour chaque terme de la somme, tu regarde quel est le terme en x^n (si tu ne t'es pas gourré il "saute aux yeux" car tu as dérivé n fois un polynôme de degrés 2n donc....)
2) pour chaque terme de la somme, tu regarde quel est le terme en x^n (si tu ne t'es pas gourré il "saute aux yeux" car tu as dérivé n fois un polynôme de degrés 2n donc....)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 10 Déc 2009, 23:14
Bon, comme je vais me coucher, je te donne plus d'indics :
tu devrait trouver comme coeff de
dans }(x))
: ^nn!\bigsum_{k=0}^n\left(\matrix{n\cr k}\right)^2)
Ensuite, pour trouver la valeur que l'on te demande, tu calcule le même coefficient mais en procédant de façon différente :
a) Quel est le coeff. de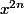
dans =x^n(1-x)^n)
?
b) En déduire le coeff de dans .
Tu termine en disant qu'évidement, les deux démarches doivent conduire au même résultat....
tu devrait trouver comme coeff de
Ensuite, pour trouver la valeur que l'on te demande, tu calcule le même coefficient mais en procédant de façon différente :
a) Quel est le coeff. de
b) En déduire le coeff de
Tu termine en disant qu'évidement, les deux démarches doivent conduire au même résultat....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :