Bonsoir,
Je bloque sur cet exercice. Pouvez-vous me donner quelques pistes?
Soit

une fonction de classe

vérifiant :
 \, + \, \frac{\partial f}{\partial y}(x,y) \, = \, e^{x+y} sin(x-y))
On considère la fonction :

 \, = \, (e^{x+y},x-y))
1. Montrer que

est bijective de

dans

.
Montrer qu'elle est

sur

.
2. On effectue le changement de variables
 \, = \psi(x,y))
. Cela revient à considérer la fonction :

définie par

, soit :
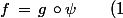)
.
En utilisant
)
, calculer les dérivées partielles de

par rapport à

et

en fonction de celles de

par rapport à

et

.
3. En déduire l'équation aux dérivées partielles vérifiée par

.
4. En déduire l'expression de

en fonction des variables

et

. Cette expression fera intervenir une fonction que l'on notera

.
5. En déduire l'expression de

en fonction des variables

et

.
Merci à vous!

