Bonjour,
J'ai un exercice que je n'arrive pas à faire en voici l'énoncé :
Une boite rectangulaire (ouverte en haut) a pour volume 32 cm2. Trouver les dimensions de la boite pour lesquelles la surface totale de la boite est minimale.
Merci d'avance,
Fonctions à deux variables
4 messages
- Page 1 sur 1
par busard_des_roseaux » 28 Nov 2007, 08:27
sûr que c'est un cube, si la boite est fermée. Mais ta boite est ouverte sur le haut, ce qui introduit une dissymétrie.
Il faut trouver le minimum de
 \longrightarrow xy+2xz+2yz)
sur la surface (variété de dimension 2) d'équation:
g(x,y,z)=xyz=32
de l'ouvert de
:
x > 0, y>0, z>0
Il me semble que les valeurs de x,y,z cherchées sont celles pour lesquelles les différentielles df et dg sont proportionnelles.
df et dg sont, toutes les deux, des applications linéaires de
dans 
)
Qui confirme ?
les calcul sont alors immédiats.
df a pour coordonnées (df/dx,df/dy,df/dz).
idem pour dg.
Il faut trouver le minimum de
sur la surface (variété de dimension 2) d'équation:
g(x,y,z)=xyz=32
de l'ouvert de
x > 0, y>0, z>0
Il me semble que les valeurs de x,y,z cherchées sont celles pour lesquelles les différentielles df et dg sont proportionnelles.
df et dg sont, toutes les deux, des applications linéaires de
Qui confirme ?
les calcul sont alors immédiats.
df a pour coordonnées (df/dx,df/dy,df/dz).
idem pour dg.
par busard_des_roseaux » 28 Nov 2007, 14:04
ok,
nous allons faire les calculs à la main car le problème est trivial. Pas besoin de fonctions implicites içi, car la surface d'équation xyz=32
admet le paramétrage global
 \longrightarrow (x,y,\frac{32}{xy}))
remarquons au passage que
est connexe par arcs puisque c'est le plan privé de l'origine et la surface itou.
la fonction à minimiser devient:
 \longrightarrow f(x,y,z)=a(x,y)=xy + \frac{64}{x}+\frac{64}{y})
En regardant la formule de Taylor:
-a(x_{0},y_{0})=h \frac{da}{dx}(x_{0},y_{0})+k \frac{da}{dy}(x_{0},y_{0})+\frac{1}{2} (h^2 \frac{d^2 a}{dx^2}(x_{0},y_{0})+2hk \frac{d^2 a}{dxdy}(x_{0},y_{0})+k^2 \frac{d^2 a}{dy^2}(x_{0},y_{0})+o(||(h,k)||^2)
on s'aperçoit que nous avons un minimum local ssi
la différentielle de a est nulle et la forme quadratique positive.
écrivons que da=0
ce qui donne
puis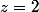 
la forme quadratique :
)
ne s'annule pas sur 
et reste positive.
conclusion: la boite est une moitié de cube. :doh:
remarque: le problème se généralise à une variété régulière,en effet le théorème des fonctions implicites fournit un paramétrage local de la variété,
, on remplace les coordonnées, du point sur la surface, via le paramètrage dans la fonction à minimiser. On différentie et l'on trouve que
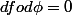et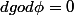 
df et dg se réduisent à deux formes linéaires de l'orthogonal de)
et sont donc proportionnelles.
cordialement,
nous allons faire les calculs à la main car le problème est trivial. Pas besoin de fonctions implicites içi, car la surface d'équation xyz=32
admet le paramétrage global
remarquons au passage que
la fonction à minimiser devient:
En regardant la formule de Taylor:
on s'aperçoit que nous avons un minimum local ssi
la différentielle de a est nulle et la forme quadratique positive.
écrivons que da=0
ce qui donne
la forme quadratique :
conclusion: la boite est une moitié de cube. :doh:
remarque: le problème se généralise à une variété régulière,en effet le théorème des fonctions implicites fournit un paramétrage local de la variété,
df et dg se réduisent à deux formes linéaires de l'orthogonal de
cordialement,
par ThSQ » 28 Nov 2007, 18:03
Une solution élémentaire : 
avec égalité ssi x=y=2z=4 (moyennes géométrique et arithmétiques).
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :