Fonction spline cube

[alexp121p]

Bonjour,
Voici un énoncé sur lequel je penche actuellement et qui demeure très difficile.

Soitn≥1eta=x0 <x1 <...<xn−1 <xn =bunesubdivisiondel’intervalleréel[a,b]enn intervalles de longueurs respectives ∆i = xi+1 − xi, 0 ≤ i ≤ n − 1 .
On appelle fonction spline cubique toute fonction s : [a, b] −→ R qui est de classe C2 sur [a, b] et telle que pour tout i ∈ {0, . . . , n − 1} et pour tout x ∈ [xi, xi+1] :
s(x)=pi(x)=αi(x−xi)3 +βi(x−xi)2 +γi(x−xi)+δi ,
avec αi, βi, γi et δi des paramètres réels. La restriction de s à l’intervalle [xi, xi+1] est donc un polynôme de degré trois, noté pi, 0 ≤ i ≤ n − 1.

1. Soit s une fonction spline cubique, écrire les contraintes qui découlent de la définition donnée au- dessus. Exprimer ces contraintes sur les coefficients αi, βi, γi et δi en fonction des ∆i, 0 ≤ i ≤ n−1. En déduire le nombre de paramètres de s non déterminés.
2. Pour la subdivision de [a,b] donnée au début et pour y = (y0,y1,...,yn) ∈ Rn+1, on suppose qu’il existe une fonction spline cubique s vérifiant s(xi) = yi pour tout 0 ≤ i ≤ n .
Montrer que l’on peut se ramener au cas où les seuls paramètres indéterminés qui restent sont αn−1 et βn−1.

Je penche déjà sur la première. Je conçois que les contraintes sont la continuité et la degré du polynôme. J'ai envisage pour exprimer ces contraintes, en ce qui concerne la continuité, d'étudier le continuité en xi et xi+1 pour S et d'étudier ensuite la dérivabilité. De faire de même pour S' pour la continuité en xi et xi+1. Est-ce une bonne piste ? Cela permettra de voir quels paramètres doivent être pris en compte.
Merci d'avance.

[alexp121p]

Soulignons que je viens juste de toucher aux fonctions spline et que cela reste encore très abstrait donc si qqn peut m'aiguiller sur leurs fonctionnements (étant curieux), je suis preneur.

[Ben314]

Salut,
Tu as fonctions avec définies respectivement sur 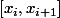et tu veut que le recollement de ces fonctions soit de classe sur donc ce qu'il faut, c'est simplement que pour tout et tout (où désigne la dérivée -ième de )

[alexp121p]

D'accord, je vois. Nous somme d'accord, ensuite, que pour prouver le degré 3 cela est intimement lié à la décidabilité ? Pour assurer la dérivabilité d'ordre 1, il est nécessaire que le polynôme fi(x) soit de degré supérieur ou égal à deux. En généralisant, on montre que pour assurer une dérivabilité jusqu'à un ordre k
, il est nécessaire que fi(x) soit un polynôme de degré supérieur ou égal à k+1 ?
Par ailleurs, pour trouver les contraintes sur les coefficients, il faut donc que je calcule les différentes égalités des Pi*(k)(xi+1)=Pi+1(k)(xi+1) pour k appartenant à l'ensemble 0,1,2 ?

[Ben314]

Je suis pas sûr de bien comprendre la question (en particulier ce que vient faire la notion de décidabilité là dedans), mais si ce que tu dit, c'est que lorsque l'on demande à ce que les recollement soit de classe C^k, il faut prendre des polynômes de degré au moins k+1 alors effectivement : si on prenait des polynômes de degré au plus k alors le fait qu'ils se recollent de façon C^k imposerait que ce soit le même polynôme sur tout les intervalles donc ça serait sans grand intérêt (et la subdivision ne servirait plus à rien).

[alexp121p]

*dérivabilté au lieu de décidabilité (correcteur automatique).
Oui, ce que vous dites est juste et c'est ce que je souhaitais écrire formellement pour en déduire les contraintes ensuites.
néanmoins, j'ai du mal à voir les contraintes syur les coefficients αi, βi, γi et δi en fonction des ∆i, 0 ≤ i ≤ n−1. Qu'entendent-ils par là ? Il faut que s soit C2 et de degré 3, mais qu'est-ce que cela implique vraiment sur ces coefficients ? Je conçois qu'il faut que ces coefficients soient différents de 0 sinon le degré 3 ne serait pas respecté mais que faut-il ajouter de plus ?

[Ben314]

Vu que on a
Et d'un autre coté, on a .
Donc la condition s'écrit
Idem pour les dérivées puis pour les dérivées secondes.

[alexp121p]

Ok, j'ai donc réussi la première question néanmoins je ne vois pas comment aborder la seconde, auriez-vous une idée ?

[Ben314]

Des inconnues, tu en a 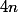(les coeffs. avec ).
Des contraintes (=équations) pour que ça se recolle correctement, la question 1) t'en a donné qui sont très clairement indépendantes donc jusque là, il y a degrés de libertés.
Si en plus tu impose que (connu), ça te fait 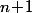contraintes supplémentaires et il est de nouveau évident qu'elles sont indépendantes des autres donc il te reste degrés de libertés et le seul truc à vérifier c'est que la connaissance de 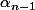et permet bien de déterminer (en cascade) toutes les autres valeurs.

Bref, as-tu écrit proprement les contraintes que tu as ?
Si c'est le qui te dérange, commence par le cas plus simple 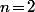où il n'y a que 2 fonctions et 3 points : ça t'éclairera.