Fonction exponentielle intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
janss
- Messages: 5
- Enregistré le: 03 Jan 2011, 21:23
-
par janss » 03 Jan 2011, 21:43
Bonsoir,
j'essaye de démontrer que la fonction exponentielle intégrale définie par :
est égale à :
Pour ce faire,
j'ai réussi à montrer que
 - ln(x) = \sum_{k=1}^{\infty} x^k/(k.k!) + K)
et je veux maintenant montrer que K est la constante d'Euler.
Je m'aide du fait que, lorsque x tend vers moins l'infini, Ei(x) = 0, donc j'ai
quand x tend vers -
,
+ \int\limits_{0}^{x}(1-exp(t))/t . dt))
et le but étant de montrer, je pense, que :
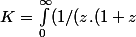)-exp(-z)/z).dz))
, ie K = gamma.
Mais je trouve que :
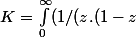)-exp(-z)/z).dz))
Merci de votre aide.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
par arnaud32 » 04 Jan 2011, 10:27
comment definis tu ln(x) pour x<0? pour faire ta limite en -oo.
-
janss
- Messages: 5
- Enregistré le: 03 Jan 2011, 21:23
-
par janss » 04 Jan 2011, 10:47
Oui j'avais remarqué que cela paraissait étonnant mais après je me débrouillais pour faire :
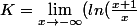 - ln (1+x) + \int\limits_{0}^{x}\frac{1-exp(t)}{t}dt))
soit
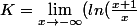 + \int\limits_{0}^{x}\frac{1-exp(t)}{t}- \frac{1}{t+1}dt))
et la le log tend vers 0...
En fait je ne vois pas d'autres moyens que de s'aider de la lim de Ei en moins l'infini car je n'ai pas d'autres valeurs remarquables de Ei pour pouvoir trouver la valeur de K
Merci !
-
janss
- Messages: 5
- Enregistré le: 03 Jan 2011, 21:23
-
par janss » 04 Jan 2011, 11:03
Merci de ton aide.
En fait, il faut comprendre l'intégrale en termes de valeur principale de Cauchy
=\lim_{\epsilon \to 0} (\int\limits_{-\infty}^{\epsilon}\frac{exp(t)}{t}dt+\int\limits_{\epsilon}^{x}\frac{exp(t)}{t}dt))
(cf :
http://fr.wikipedia.org/wiki/Valeur_principale_de_Cauchy)
Sinon j'ai déjà regardé ton lien et c'est pour ca que je veux m'aider du fait que :
}-\frac{exp(-z)}{z})dz)
Pour expliquer d'où proviens mon égalité sur K :
j'ai fait :
 - ln (x) = \int\limits_{0}^{x}\frac{exp(t)-1}{t}dt + constante)
(on obtient cette égalité en intégrant la dérivée de Ei(x)-ln(x).
Donc j'isole la constante (K) et j'ai donc :
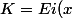 - ln (x) -\int\limits_{0}^{x}\frac{exp(t)-1}{t}dt)
La j'étudie la limite en -00 pour enlever Ei(x) d'où l'égalité que j'avais tout à l'heure :
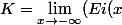 - ln (x) -\int\limits_{0}^{x}\frac{exp(t)-1}{t}dt))
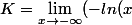 -\int\limits_{0}^{x}\frac{exp(t)-1}{t}dt))
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
par arnaud32 » 04 Jan 2011, 12:37
c'est quand meme bizarre de definir ta fonctio pour x>0 et de faire tendre x vers -oo
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 04 Jan 2011, 12:48
Pour x >= 0, Ei(x) est une intégrale d'un truc pas intégrable... ; quant à ln(x), il existe pas quand x<=0.
Donc Ei(x) - ln(x) ça veut rien dire, pour aucun x.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 04 Jan 2011, 12:57
Même pour la valeur principale, Ei(0) n'existe pas. Donc tu sais ptetre que pour x>0, la différence est une constante K, mais tout ton discours n'apporte rien si tu veux parler de ce qui se passe quand x < 0.
(surtout avec log(x) qui n'existe pas)
(e^t-1)/t est définie sur R mais n'est pas intégrable en -l'infini.
Et pour ses deux morceaux, e^t/t et 1/t ne sont pas intégrables en 0. (mais on peut toujours parler de leur valeur principale)
-
janss
- Messages: 5
- Enregistré le: 03 Jan 2011, 21:23
-
par janss » 04 Jan 2011, 13:24
Oui je suis d'accord. J'avais vu cette façon de proceder sur internet mais cela me paraissait étonnant.
Vous avez une idée pour trouver K ?
Merci
-
Ben314
- Le Ben
- Messages: 21696
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 04 Jan 2011, 15:28
Salut,
Pour tout
, on a :
\ <br />=\ {\rm Ei}(1)\ +\ \int_1^x\frac{\exp(t)}{t}\,{\rm d}t\ <br />=\ {\rm Ei}(1)\ +\ \ln(x)\ +\ \int_1^x\frac{\exp(t)-1}{t}\,{\rm d}t)
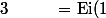\ +\ \ln(x)\ +\ \int_1^0\frac{\exp(t)-1}{t}\,{\rm d}t\ +\ \int_0^x\left(\sum_{k\geq 1}\frac{t^{k-1}}{k!}\right){\rm d}t\ <br />=\ \ln(x)\ +\ \sum_{k\geq 1}\frac{x^k}{k k!}\ +\ {\rm C})
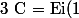\ -\ \int_0^1\frac{\exp(t)-1}{t}\,{\rm d}t\ <br />=\ \int_{-\infty}^{-1}\frac{\exp(t)}{t}\,{\rm d}t\ +\ \lim_{\epsilon\to0^+}\left(<br />\int_{-1}^{-\epsilon}\frac{\exp(t)}{t}\,{\rm d}t+\int_{\epsilon}^1\frac{\exp(t)}{t}\,{\rm d}t\right)\ -\ \int_0^1\frac{\exp(t)-1}{t}\,{\rm d}t)
}{t}\,{\rm d}t\ +\ <br />\int_0^{1}\frac{-\exp(-t)+\exp(t)}{t}\,{\rm d}t\ -\ \int_0^1\frac{\exp(t)-1}{t}\,{\rm d}t\ <br />=\ -\int_{1}^{\infty}\frac{\exp(-t)}{t}\,{\rm d}t\ +\ <br />\int_0^{1}\frac{1-\exp(-t)}{t}\,{\rm d}t)
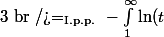\exp(-t)\,{\rm d}t\ -\ <br />\int_0^{1}\ln(t)\exp(-t)\,{\rm d}t\ <br />=\ -\int_0^{\infty}\ln(t)\exp(-t)\,{\rm d}t\ =\ \gamma)
(c.f. par exemple le capes 2010 pour cette dernière égalité)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
JeanJ
- Membre Relatif
- Messages: 264
- Enregistré le: 09 Jan 2010, 09:04
-
par JeanJ » 04 Jan 2011, 16:35
Dans ces formules, il faut comprendre ln(x) comme étant ln(abs(x)).
Il faut comprendre les intégrales en tant qu'intégrales de Cauchy (comme cela a déjà été signalé)
Pas de problème sur tous les réels excepté 0.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 04 Jan 2011, 18:10
et remarquer que
=1-\gamma+\sum_1^{\infty}\frac1{n(n+1)}=-\gamma)
-
janss
- Messages: 5
- Enregistré le: 03 Jan 2011, 21:23
-
par janss » 05 Jan 2011, 00:45
Merci beaucoup, c'est super !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
