Fonction différentielle

[Scipion]

Bonjour à tous, je suis confronté au problème suivant :

Je dois étudier la différentiabilité de la fonction suivante :
f(x,y) = (x² * y) / (x²+y²)

La fonction est bien continue. Cependant, dans mes solutions, je vois que cette fonction n'est pas différentiable en (0,0). Je ne comprends pas, car une fonction qui est bien continue et dont ses dérivées partielles existent n'est-elle pas différentiable ? Comment se fait-il que cette fonction ne le soit pas ? Si quelqu'un a une idée, merci beaucoup :).

[SimonB]

Non, une fonction continue et dont les dérivées partielles existent n'est pas forcément différentiable, et tu en as un des contre-exemples les plus simples !

En revanche, si les dérivées partielles existent et sont continues, ta fonction est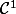 (non seulement la différentielle existe, mais elle est continue).

[Scipion]

Très bien je vois. Et pour savoir si une dérivée partielle est continue, je dois tout développer, enfin faire la dérivée en x et en y, simplifier et remplacer (ici par mon 0,0). Je veux dire, il n'y a pas de moyen plus simple qui me permettrait en quelques sortes de voir très rapidement si les dérivées partielles sont continues ?