Fonction Arccos (cos x)

[joquetino]

Bonjour,

Je suis en train de faire des tests sur Internet sur les fonctions arccos et arcsin.
Je dois écrire les fonction arccos et arcsin sous la forme x=a+bπ.

On sait que Arccos cos X = X si X est entre 0 et Pi.
On a la même chose pour arcsin sin x = X pour X entre -Pi/2 et Pi/2.

Il faut donc revenir à un intervalle connu dans mon exo.

Si je prend un exemple :
x= arccos (cos (10,4)) .

Je comptais l'écrire : x = 10.4 - 3 Pi

Or la réponse est : x = -10.4 + 4 Pi

Une chose doit m'échapper car je ne comprend pas la solution, ou en tout cas, je ne comprend pas pourquoi ma réponse est fausse. Pouvez-vous m'éclairer ?

Merci d'avance

[vladi]

Bonjour

ça ne va pas car il faut que vous utilisiez la congruence

avant de vous servir de arccos il faut que vous calculiez et prendre y pour argument de arccos

lorsque

lorsque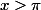 et alors

sinon

[vladi]

coquille

je voulais dire prendre y pour argument de cos

[joquetino]

Bonsoir,

Merci pour la réponse. A vrai dire, je ne connaissais plus les congruences ou en tout cas, j'ai oublié depuis plus de 15 ans sans maths.
Est-ce possible de m'expliquer le sens de cette congruence dans le cadre de cet exercice ? Ou peut-être un lien qui me l'explique ? Je ne voudrais pas utiliser "bêtement" une formule sans la comprendre.
Sinon, quelle est la formule pour arcsin sinx ? X doit être entre -Pi/2 et Pi/2.

Par exemple : x=arcsin(sin(4.2))

Merci bcp.

[vladi]

Ou peut-être un lien qui me l'explique ? Je ne voudrais pas utiliser "bêtement" une formule sans la comprendre.

bonjour non je n'ai pas de lien (j'ai rien en fait ) mais en fait il n'y a rien à comprendre de compliqué

j'ai juste oublié de dire que dans le propos ici

revient tout simplement à dire qu'un quelconque réel x est équivalent à y dans l'intervalle si et seulement si

et

quand à la formule qui donne y pour l'expliquer en gros vous savez que la somme de la partie entière inférieure et de la partie fractionnaire de tout reel positif est ce réel là

à partir de là en manipulant un peu ça vous arrivez à la formule

[lyceen95]

Arccos (cos x) = x quand x est entre 0 et Pi. Ok.
La fonction cos est périodique , de période 2 Pi.

Si on connait le comportement de Arccos(cos(x)) sur un segment de longueur 2Pi, grâce à cette périodicité 2Pi, on connaîtra le comportement de cette fonction sur R tout entier.
Mais pour l'instant, on ne connait son comportement que sur [0, Pi], c'est à dire un segment de longueur Pi seulement.
Il nous faudrait le comportement de Arccos(cos(x)) sur [-Pi ,0] , ou sur [Pi ,2Pi] pour connaitre parfaitement cette fonction.
Et comme la fonction cos est paire, trouver le comportement de Arccos(cos(x)) sur [-Pi ,0] , ça devrait être facile.

[tournesol]

C'est très facile:
Il suffit de savoir que arccos(cos x)=x sur [0;pi] et que arccos(-X)=2pi-arccos(X) sur [0;pi] .
Pour k dans Z , si x appartient à [kpi;(k+1)pi] , alors x-kpi est dans [0;pi] et donc arccos(cos(x-kpi)=x-kpi
Or cos (x-kpi)=(-1)^k cos x
Si k est pair , arccos(cos x)=x-kpi
Si k est impair , 2pi - arccos(cos x)=x-kpi nous donne arccos(cos x)=(k+2)pi -x

[joquetino]

Merci à vous pour vos réponses.

[tournesol]

arccos(-X)=pi-arccos Xet non pas 2pi-arccos X
désolé .