Fonction analytique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 15 Mai 2007, 20:17
par nemesis » 15 Mai 2007, 20:17
bonsoir a tous
quelqu'un peut-il me rappeler comment on trouve que :
 + cos(2x) + cos(3x) +..........+cos(nx) \le \frac{1}{sin (x/2)})
et comment montrer que la fonction h(x) définie par
=\sum_{n=1}^\infty e^{-n} e^{i n^2 x})
n'est pas analytique au voisinage de 0 ?
merci d'avance
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Mai 2007, 20:23
par fahr451 » 15 Mai 2007, 20:23
bonsoir
pour l'inégalité
tu calcules exp(ix) +...+exp(inx) somme géométrique
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 15 Mai 2007, 20:32
par road runner » 15 Mai 2007, 20:32
ouai ca donne

ensuite on remplace
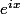
par cos x+ i sin x ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Mai 2007, 20:41
par fahr451 » 15 Mai 2007, 20:41
pour l'autre question
j'ai une solution dont je suis guère satisfait et qui n'est pas si rapide à exposer
tu as eu la question ainsi ?
je t'explique les grandes lignes
h est C infini on peut dériver terme à terme en 0
h^(p) (0) = i^p a(p)
si h était analytique on aurait
h (x) = sigma i^p x^p a(p) /p! de rayon de cv non nul
et là je montre avec des majorations minorations pas si simples
que a(p+1)/[(a(p)p] ->+infini ce qui donne (d'après d'alembert )un rayon de cv nul
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 15 Mai 2007, 20:48
par nemesis » 15 Mai 2007, 20:48
je t'expose dans quelque instant ce que je fais (le temps d'ecrire tous ca en latex ,sinon c'est illisible)
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 15 Mai 2007, 21:14
par nemesis » 15 Mai 2007, 21:14
une question avant si on montre que la serie
}(0)}{k!} x^k)
est divergente alors h n'est pas analytique ?
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 15 Mai 2007, 21:55
par nemesis » 15 Mai 2007, 21:55
en partant du principe que si la serie
} (0)|}{k!} x^k)
est divergente alors h n'est pas analytique
je me lance :
on a :
} (0) =\sum_{n=0}^\infty i^(k) e^{-n} n ^2k \\ \frac {h^{(k)} (0) }{k!}=\frac {i^k}{k!}\sum_{n=0}^\infty e^{-n} (n ^2)^k)
en module on a :
^k)
et :
} (0) }{k!} x^k\ge 1/k! \sum_{1}^N e^{-n} (n^2)^k x^k)
x dans le voisinage de 0 et x>0,
en sommant on a:
} (0) }{k!} x^k\ge \sum_{k=0}^\infty 1/k! \sum_{1}^N e^{-n} (n^2)^k x^k \\ \ge \sum_{k=0}^N \sum_{1}^\infty 1/k! e^{-n} (n^2)^k x^k \\ \ge \sum_{k=0}^N e^{-n} \sum_{1}^\infty \frac {(n^{2} x)^k}{k!} \\ \ge \sum_{k=0}^N e^{-n} e^{n^2x} = \sum_{k=0}^N e^{n^x} \text {qui est divergente (terme general tendant vers l'infinie))
et donc la serie
} (0)|}{k!} x^k)
est divergente (superieur a une serie qui diverge ,donc pas analytique,bonne lecture
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Mai 2007, 22:09
par fahr451 » 15 Mai 2007, 22:09
alors
pour moi il y a un problème dans ce que tu as écrit
après "en sommant"
k varie de 0 à +infini et n de 1 à N ( N fixé je présume)
et la ligne d 'après les bornes changent
as tu permuté les sigma ? je le pense si oui
c'est >= sigma n = 1 à N de sigma k = 0 à +infini
et à la fin c 'est sigma de exp (-n+n^2x)
ceci dit c 'est TRES BIEN
une remarque en fait en regardant la série initiales avec les modules partout
il est inutile de couper à N on peut travailler avec la série double de réels positifs qui existe toujours dans RU {+infini}
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 15 Mai 2007, 22:19
par nemesis » 15 Mai 2007, 22:19
ok merci a toi :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités