Fonciton périodique non constante admet une + petite periode

[MoonX]

Bonjour,

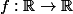
Soit une fonction continue, périodique, non constante.
Montrer que la fonction f admet une plus petite période.

Je ne sais pas comment commencer. J'ai pensé aux sous groupes additifs de R, mais j'aimerai trouver une preuve plus élémentaire ( en considérant l'ensemble des périodes de f)

[aviateur]

Bonjour Voilà comment je commencerai:
On dit que T>0 est une période pour f ssi f(x+T)=f(x) pour tout x ds R.
Soit E l'ensemble des périodes de f et

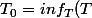T_0 est bien défini puisque E est non vide et minoré par 0.
Reste à montrer que T_0 est une période.

[MoonX]

Merci pour votre réponse.
Soit une suite d'éléments de (l'ensemble des périodes de f) qui tend vers T_0 (par caractérisation de la borne inf).

alors et par continuité.

Donc T_0 est bien une période.
Mais je vois pas où l'hypothèse "Non constante" entre en jeux ???

[Viko]

@MoonX si f est constante inf{Per(f)} n'est pas bien définie

[MoonX]

Faut-il nécessairement supposer que 0 n'est pas période ? C'est ça que j'ai du mal à comprendre :
Pourquoi 0 ne serait-il pas période ? (ce qui est vrai pour toute fonction continue) Ou alors ma définition de période est erronée ?

[Viko]

il est juste de dire qu'une fonction est 0-périodique, et c'est clairement vrai pour toute fonction donc autant ne pas le préciser (je n'ai pas fait de recherche approfondi sur le sujet donc je me trompe peut-être)

[Kolis]

Bonjour !
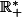
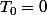
La borne inférieure d'une partie de peut très bien être nulle. Et n'est pas très utile....
....................................................................................
Je ne vois pas comment tu pourrais te passer des propriétés des groupes additifs de !
Si tu supposes le groupe des périodes dense, soit .
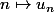
Il existe une suite d'éléments de qui converge vers .
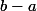
Comme et continue, par limite on aura .