Ou es ma faute??

par **aviateurpilot** » 23 Sep 2006, 09:47

salut les amis
je voulais trouvrer tt les fonction derivable 2 fois tel que
(*)

je veux savoir ou es ma faute

donne

si f(0)=0 alors f(x)=0 quelque soit x
si f(0)=1
on a

si y==>0
on trouve

donc

g(x)=cosx verifie (*)
mais

et

merci d'avance

par **tize** » 23 Sep 2006, 09:57

Salut,
Il me semble qu'en faisant tendre y vers 0 dans :

on a pas

mais plutôt 0 !
Il aurait fallu qu'il y ai

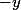
au deuxième dénominateur...non ?

par **tize** » 23 Sep 2006, 10:12

J'explicite mon dernier post :

par **aviateurpilot** » 23 Sep 2006, 10:45

si y=>0+ -y=>0- c'est ma faute

merci