Extrema et points d'inflexion.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 21 Mai 2012, 15:35
par Deluxor » 21 Mai 2012, 15:35
Bonjour à tous!
J'ai quelques questions sur les extrema et points d'inflexion d'une fonction.
"En utilisant le critère de la dérivée première, trouver, s'il en existe, les extrema locaux de la fonction  \, = \, \frac{1}{9}x^3 \, - \, \frac{1}{6}x^2 \, - \, \frac{2}{3}x \, + \, 1) "
"Les extrema locaux éventuels de

sont les solutions de
 = 0)
, c'est-à-dire
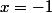
ou
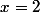
.
L'énoncé appelle-t-il à prouver s'ils le sont vraiment? Si oui, comment prouver qu'ils le sont bien?
----------
"Déterminer les points d'inflexion éventuels de la fonction  \, = \, (x-1)^{\frac{1}{3}}) "
"Pour cela, suffit-il de trouver les points

qui annulent
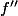
?
Merci à vous!

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Mai 2012, 15:52
par Dinozzo13 » 21 Mai 2012, 15:52
Salut !
Deluxor a écrit:Pour cela, suffit-il de trouver les points

qui annulent
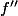
?
Merci à vous!

Tout à fait : les points d'inflexion sont solutions de l'équation
=0)
:+++:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Mai 2012, 15:54
par chan79 » 21 Mai 2012, 15:54
Deluxor a écrit:Bonjour à tous!
J'ai quelques questions sur les extrema et points d'inflexion d'une fonction.
"En utilisant le critère de la dérivée première, trouver, s'il en existe, les extrema locaux de la fonction  \, = \, \frac{1}{9}x^3 \, - \, \frac{1}{6}x^2 \, - \, \frac{2}{3}x \, + \, 1) "
"Les extrema locaux éventuels de

sont les solutions de
 = 0)
, c'est-à-dire
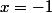
ou
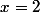
.
L'énoncé appelle-t-il à prouver s'ils le sont vraiment? Si oui, comment prouver qu'ils le sont bien?
----------
"Déterminer les points d'inflexion éventuels de la fonction  \, = \, (x-1)^{\frac{1}{3}}) "
"Pour cela, suffit-il de trouver les points

qui annulent
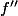
?
Merci à vous!

Salut
Tu peux déjà faire le tableau de variations
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 21 Mai 2012, 15:56
par Skullkid » 21 Mai 2012, 15:56
Bonjour, pour la première question, l'énoncé te demande bien de trouver les extremums locaux de f, pas les candidats extremums locaux, donc une fois que tu as trouvé les candidats, il faut vérifier s'ils sont bien extremums locaux. Si x est un de ces candidats et que f' change de signe en x, alors c'est un extremum local. Sinon, ça n'en est pas un.
Pour les points d'inflexion c'est le même principe, tu trouves les candidats en résolvant f''(x) = 0, et ensuite tu dois vérifier si tes candidats sont des points d'inflexion ou pas, en regardant si f'' change de signe.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
