fait c... : je trouve pas de méthode simple et élégante (alors que je pense qu'il y en a une...)
Donc (pas beau... :hum:) on considère des réels strictement positifs

fixés et on cherche les angles

tels que
^2+\big(\sum_{k=1}^n \rho_k\cos\theta_k\big)^2)
soit minimale.
Si on dérive
par rapport à la variable
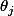
(là, je sais pas si je sort pas légèrement du programme...) on trouve :
)
Les deux termes d'indice

dans les deux sommes s'éliminent donc

où

et

sont positifs et ne dépendent pas de
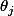
.
On en déduit que, par rapport à la variable
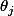
, la fonction
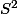
est croissante puis décroissante sur
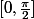
et donc que son minimum sera atteint pour

ou bien

Le minimum de la fonction
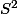
(où je rappelle que les

sont fixés) sera donc atteint lorsque tout les
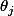
sont dans le doubleton

. Dans ce cas, en séparant la somme en deux (les

t.q.

d'un coté et ceux telles que

de l'autre), on a :
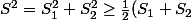^2=\frac{1}{2}\Big(\sum_{k=1}^n\rho_k\Big)^2)