Question de colle sur les complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 15 Déc 2013, 17:16
par Victhemath » 15 Déc 2013, 17:16
Bonsoir, j'ai la question de colle suivante pour la semaine prochaine :
Montrer que
)
et
)
sont des groupes.
Quelqu'un peut m'aider ? Sachant que le premier groupe c'est l'ensemble des nombres complexes tels que leur module égale 1 et l'autre, c'est semble des racines n-ième de l'unité.
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 15 Déc 2013, 18:01
par jonses » 15 Déc 2013, 18:01
Victhemath a écrit:Bonsoir, j'ai la question de colle suivante pour la semaine prochaine :
Montrer que ) et
et) sont des groupes.
sont des groupes.Quelqu'un peut m'aider ? Sachant que le premier groupe c'est l'ensemble des nombres complexes tels que leur module égale 1 et l'autre, c'est semble des racines n-ième de l'unité.
Bonjour,
J'imagine que

signifie la loi de composition interne

sur

Au choix, soit tu montres que ces deux ensembles munis de la lci

vérifient les propriétés d'un groupe (associativité, existence d'un élément neutre, tout élément admet un symétrique), soit que ce sont des sous-groupes de

-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 15 Déc 2013, 18:10
par Victhemath » 15 Déc 2013, 18:10
Merci

J'ai une nouvelle question, je dois calculer :

-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 15 Déc 2013, 18:29
par Maxmau » 15 Déc 2013, 18:29
Victhemath a écrit:Merci

J'ai une nouvelle question, je dois calculer :

Bj
Les éléments de Un sont les racines du polynôme X^n - 1
Comment calculer la somme des racines d'un polynôme à partir de ses coefficients ?
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 15 Déc 2013, 18:40
par jonses » 15 Déc 2013, 18:40
Victhemath a écrit:Merci

J'ai une nouvelle question, je dois calculer :

Soit n un entier naturel non nul,
S=

=
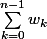
mais
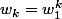
c'est donc une somme en...
donc (si n=1) S=... ou (si n>1) S=....= 0 car
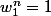
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 15 Déc 2013, 21:13
par Victhemath » 15 Déc 2013, 21:13
On a ici

donc w appartient à l'ensemble des racines n-ièmes de l'unité. Votre réponse correspond bien à cela ?
Merci de votre réponse.
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 15 Déc 2013, 21:32
par Sourire_banane » 15 Déc 2013, 21:32
Victhemath a écrit:Merci

J'ai une nouvelle question, je dois calculer :

Ouaouh jamais vu ce genre d'écritures

Sinon plus sérieusement ça fait 0 parce que somme géométrique (sauf erreur). Ou sinon tu exploites le fait que le polynôme donné par Maxmau est scindé sur C.
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 15 Déc 2013, 23:26
par Victhemath » 15 Déc 2013, 23:26
Ca fait 0 sauf si n=1 et au quel cas, on a la somme égale à 1.
J'ai la même chose avec :

C'est la même méthode ?
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 16 Déc 2013, 06:49
par jonses » 16 Déc 2013, 06:49
Victhemath a écrit:Ca fait 0 sauf si n=1 et au quel cas, on a la somme égale à 1.
J'ai la même chose avec :

C'est la même méthode ?
Explicite cette somme, tu remarqueras que c'est une somme en progression géométrique
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 16 Déc 2013, 08:52
par Maxmau » 16 Déc 2013, 08:52
Victhemath a écrit:Ca fait 0 sauf si n=1 et au quel cas, on a la somme égale à 1.
J'ai la même chose avec :

C'est la même méthode ?
on peut aussi remarquer que c'est une fonction symétrique des racines de X^n - 1. Cette somme s'exprime donc en fonction des coefficients du polynôme X^n - 1.
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 17 Déc 2013, 21:59
par Victhemath » 17 Déc 2013, 21:59
Nouvelle question de colle !

J'ai

donner la définition de
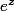
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 17 Déc 2013, 22:18
par jonses » 17 Déc 2013, 22:18
Victhemath a écrit:Nouvelle question de colle !

J'ai

donner la définition de
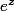
Comme

on dispose de

tels que
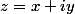
alors
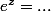
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 17 Déc 2013, 22:32
par Victhemath » 17 Déc 2013, 22:32
jonses a écrit:Comme

on dispose de

tels que
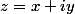
alors
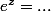
Ha mais je m'attendais à quelque chose de compliqué.. Il faut donner la partie réelle, imaginaire etc ?

avec re(z)=e^a et im(z)=e^b ? Qu'entendent-ils par définition ?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 17 Déc 2013, 22:44
par Sourire_banane » 17 Déc 2013, 22:44
Victhemath a écrit:Ha mais je m'attendais à quelque chose de compliqué.. Il faut donner la partie réelle, imaginaire etc ?

avec re(z)=e^a et im(z)=e^b ? Qu'entendent-ils par définition ?
Ben la définition d'une fonction c'est la donnée de son ensemble de départ et d'arrivée, de son expression algébrique et éventuellement de ses propriétés.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Déc 2013, 23:13
par Ben314 » 17 Déc 2013, 23:13
Salut,
Je sais pas du tout à quel niveau on voit ça, mais je trouve que ça fait un peu moins "bricolage" de prendre comme définition
=\sum_{n\geq 0}\frac{z^n}{n!})
.
En particulier, ça permet d'avoir la même définitions pour les réels, les imaginaires purs, les complexes, les quaternions, les matrices, etc, etc...
Alors que, si on me disait que la définition c'est
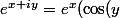+i\sin(y)))
, je pense que je répondrait instantanément "et la définition de cos(y), c'est quoi ?"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 17 Déc 2013, 23:16
par Victhemath » 17 Déc 2013, 23:16
Merci à vous deux ! j'y penserai demain si je tombe dessus !
Ben, cette formule me dit quelque chose mais cette définition semple pas pour l'instant être dans le programme de sup, je la retiens, elle est intéressante :)
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 18 Déc 2013, 19:40
par jonses » 18 Déc 2013, 19:40
Désolé pour le retard,
Je pensais Victemath que tu avais vu ce qu'était la fonction exponentielle complexe donc j'ai pas mis la réponse d'emblée (encore désolé)
Si je reprends les notations que j'ai posées on a en fait
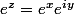
(c'est peu-être comme ça que tu as dû le voir en cours, en tout cas c'est comme ça que je l'ai vu)
Et à partir de là tu peux en déduire plusieurs propriété de la fonction exponentielle complexe etc.
C'est peut-être tout ça qu'on te demandait ?
Ben314 a écrit:Salut,
Je sais pas du tout à quel niveau on voit ça, mais je trouve que ça fait un peu moins "bricolage" de prendre comme définition
=\sum_{n\geq 0}\frac{z^n}{n!})
.
Ce que te propose Ben314 c'est bel et bien vu en sup (en tout cas pour la fonction exponentielle réelle) et, dans le cadre des réels en tout cas, c'est le développement limité à l'ordre n de la fonction exponentielle
(reprenez-moi si je dis des bêtises, ça m'arrive souvent)
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 18 Déc 2013, 20:23
par Victhemath » 18 Déc 2013, 20:23
Ha oui, je me disais aussi, c'est bien son DL ! Et pour ce qui est de la définition, un camarade à moi est tombé dessus et il fallait donner la partie réelle, imaginaire etc.. :)
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 19 Déc 2013, 18:43
par jonses » 19 Déc 2013, 18:43
jonses a écrit:Ce que te propose Ben314 c'est bel et bien vu en sup (en tout cas pour la fonction exponentielle réelle) et, dans le cadre des réels en tout cas, c'est le développement limité à l'ordre n de la fonction exponentielle
Excuse-moi, je crois bien que j'ai dit une horreur, ça ressemble au dl de exponentielle (la différence avec le dl, c'est que dans le dl "on s'arrête" à un certain ordre n et on rajoute un reste qui est négligeable devant

)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
et
sont des groupes.
avec re(z)=e^a et im(z)=e^b ? Qu'entendent-ils par définition ?
.