Bonjour,
Je bloque sur cet exercice. Je parviens à faire le 1 en considérant une symétrie ortho mais ça me parait trop compliqué. Et je n'arrive à rien sur la question 2.
Merci d'avance pour vos réponses ou pistes.
J.P.
On considère un espace euclidien de dimension n.
1. Soit x un vecteur de norme "racine de n".
Montrer qu'il existe une base orthonormée de E dans laquelle les coordonnées de x sont (1,...,1).
2. Si norme de x vaut racine de n, norme de y vaut racine de 1+2^2+...+n^2 et (x|y)=1+2+...+n,
montrer l'existence d'une BON de E dans laquelle les coord. de x sont (1,1,..,1) et celle de y: (1,2,...,n).
Existence d'une Base orthonormées
7 messages
- Page 1 sur 1
Re: Existence d'une Base orthonormées
salut
dans une telle base (e_1, e_2, ..., e_n) alors on a
(x, e_1) = 1
(x, e_2) = 1
...
(x, e_n) = 1
avec (e_i, e_j) = 1 si i = j et = 0 si i <> j
...
dans une telle base (e_1, e_2, ..., e_n) alors on a
(x, e_1) = 1
(x, e_2) = 1
...
(x, e_n) = 1
avec (e_i, e_j) = 1 si i = j et = 0 si i <> j
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Existence d'une Base orthonormées
Salut,
Si tu regarde ton truc de façon théorique, ben en fait c'est des cas particulier (avec m=1 et m=2) d'un résultat qu'on pourrait énoncer comme suit :
- Est ce que tu voit comment démontrer un tel théorème ?
P.S. : Si ça te semble trop théorique, on peut tenter de le faire "plus à la main", mais les idées seront les mêmes.
Si tu regarde ton truc de façon théorique, ben en fait c'est des cas particulier (avec m=1 et m=2) d'un résultat qu'on pourrait énoncer comme suit :
- Est ce que tu voit pourquoi ça répond aux deux questions ?Théorème a écrit:Si dans un espace Euclidienon a deux familles de vecteurs
et
telles que, pour tout
on ait
alors il existe au moins une isométrie vectorielle
(i.e. un élément du groupe orthogonal) telle que
pour tout
.
- Est ce que tu voit comment démontrer un tel théorème ?
P.S. : Si ça te semble trop théorique, on peut tenter de le faire "plus à la main", mais les idées seront les mêmes.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Existence d'une Base orthonormées
Salut,
Je vois comment démontrer ce résultat, je vois comment il s'applique au 1, mais pas au 2.
Je ne vois pas comment trouver un endo orthogonal qui match pour les 2 familles.
Je vois comment démontrer ce résultat, je vois comment il s'applique au 1, mais pas au 2.
Je ne vois pas comment trouver un endo orthogonal qui match pour les 2 familles.
Re: Existence d'une Base orthonormées
En admettant ça :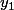 donné par l'énoncé dont tu sait uniquement que
donné par l'énoncé dont tu sait uniquement que  et d'un autre coté, si tu prend une b.o.n.
et d'un autre coté, si tu prend une b.o.n. 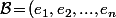) quelconque de
quelconque de  et le vecteur
et le vecteur  de coordonnées
de coordonnées ) dans
dans 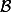 alors on a
alors on a  .
.
En vertu du théorème, il existe donc une isométrie vectorielle de
de  telle que
telle que \!=\!y_1) ce qui montre que
ce qui montre que 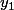 a pour coordonnées
a pour coordonnées ) dans la b.o.n.
dans la b.o.n. \!=\!\big(f(e_1),f(e_2),...,f(e_n)\big))
Pour le 2), exactement pareil : les deux vecteurs donnés de l'énoncé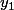 et
et 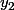 sont tels que :
sont tels que :

Or, si tu prend une b.o.n.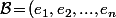) quelconque de
quelconque de  et les vecteur
et les vecteur 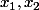 de coordonnées respectives
de coordonnées respectives ) et
et ) dans
dans 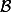 alors tu as :
alors tu as :
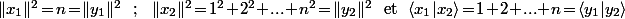 .
.
Donc en vertu du théorème, il existe donc une isométrie vectorielle de
de  telle que
telle que \!=\!y_1) et
et \!=\!y_2) ce qui montre que
ce qui montre que 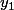 et
et 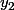 ont pour coordonnées respectives
ont pour coordonnées respectives ) et
et ) dans la b.o.n.
dans la b.o.n. \!=\!\big(f(e_1),f(e_2),...,f(e_n)\big)) .
.
Bref, les deux trucs, c'est donc bel et bien des applications directes du théorème en question et si on veut "faire un peu de théorie", c'est lui qu'il faut démontrer.
On peut aussi le faire plus "à la main" dans ces deux cas particulier (i.e m=1 et m=2), mais je pense que, comme dans le théorème général, on ne coupera pas au fait de montrer qu'il existe une isométrie vectorielle qui envoie les sur les
sur les  et c'est bien exactement ce que tu as fait pour le 1) où, si on veut juste envoyer un vecteur sur un autre de même norme, il suffit de considérer une isométrie orthogonale.
et c'est bien exactement ce que tu as fait pour le 1) où, si on veut juste envoyer un vecteur sur un autre de même norme, il suffit de considérer une isométrie orthogonale.
Pour le 1), tu as le vecteurThéorème a écrit:Si dans un espace Euclidienon a deux familles de vecteurs
et
telles que, pour tout
on ait
alors il existe au moins une isométrie vectorielle
(i.e. un élément du groupe orthogonal) telle que
pour tout
.
En vertu du théorème, il existe donc une isométrie vectorielle
Pour le 2), exactement pareil : les deux vecteurs donnés de l'énoncé
Or, si tu prend une b.o.n.
Donc en vertu du théorème, il existe donc une isométrie vectorielle
Bref, les deux trucs, c'est donc bel et bien des applications directes du théorème en question et si on veut "faire un peu de théorie", c'est lui qu'il faut démontrer.
On peut aussi le faire plus "à la main" dans ces deux cas particulier (i.e m=1 et m=2), mais je pense que, comme dans le théorème général, on ne coupera pas au fait de montrer qu'il existe une isométrie vectorielle qui envoie les
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Existence d'une Base orthonormées
Ca se fait très bien par récurrence surThéorème a écrit:Si dans un espace Euclidienon a deux familles de vecteurs
et
telles que, pour tout
on ait
alors il existe au moins une isométrie vectorielle
(i.e. un élément du groupe orthogonal) telle que
pour tout
.
- On peut considérer qu'on fait l'initialisation avec m=0 où le résultat est trivialement vrai en prenant n'importe quelle isométrie pour
- Ensuite, on fixe un m
Ensuite, si
Sinon, on considère la symétrie orthogonale
(*) Ce qui est trivial intuitivement parlant mais un soupçons long à écrire.
(**) Ce qui est légèrement moins évident intuitivement parlant mais par contre super rapide à vérifier.
Et si tu veut le faire "plus à la main", ça veut juste dire que dans le 2), on peut faire quasiment comme au 1), mais en composant deux symétries orthogonales au lieu d'en utiliser uniquement une.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
