Exercice sup theoreme de cantor

[edeniris]

bonjour je m entraine en ce moment sur divers exercice et celui ci m a posé probleme merci de m aider voici l enoncer:
Soit E un ensemble. On se propose de démontrer le théorème de Cantor : il n'existe pas d'injection de P (E) dans E.
1) on supoose qu'il existe une surjection f de E sur P (E). Soit A = (x appartient à E/ x n'appartient pas à f (x)).
Aboutir à une contradiction à l'aide de A et d'un antécédent de A par f.
2) on suppose qu'il existe une injection f de P (E) dans E. Aboutir à une contradiction

[Nightmare]

Bonsoir,

Soit f une surjection de E dans P(E) et
.

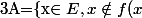Si A a un antécédent par f, il existe y tel que f(y)=A

Si y est dans A, alors y n'est pas dans f(y) ie y n'est pas dans A => Absurde
y n'est donc pas dans A, mais s'il n'est pas dans A, il est dans A => Absurde.

2)On a équivalence entre : Il existe une injection de P(E) dans E.
et
Il existe une surjection de E dans P(E).

[Nightmare]

On a aussi une très belle manière de démontrer ce théorème :

Il est clair que l'application est injective.

Supposons qu'il existe une injection de P(E) dans E. Alors vu qu'il existe une injection de E dans P(E), d'après le théorème de Cantor-Bernstein, il existe une bijection de E dans P(E). Absurde, car

:happy3:

[thedream01]

Cette démonstration n'est vraie que si E est fini, alors que le théorème est vrai pour E infini aussi...

[edeniris]

merci pour votre aide