Exercice Proba

[Mehdilis]

Bonjour, je flanche sur les 3 dernières questions. Quelqu'un pour m'aider? Merci :help:

[lulu math discovering]

Pour la question d) n'oublie pas que si tu as la possibilité 1+5, tu as aussi la 5+1 !! (et idem pour les autres)

[Mehdilis]

Pour la question d) n'oublie pas que si tu as la possibilité 1+5, tu as aussi la 5+1 !! (et idem pour les autres)

Merci de t'as réponse, je pensais à mettre pour la rep d :

(1)(1)+(3)(1)+(2)(2)+(1)(3)+(1)(1)
(1)(1)..(1)(1)..(1)(1)...(1)(1)..(1)(1)

le tout diviser par 64 Ce qui me donnerait 12/64

[lulu math discovering]

Je procèderait plutôt directement en probas. Je note X la valeur de la première boule tirée et X' celle de la deuxième tirée.

La proba d'avoir 6 en tout, c'est :

P(X=1)*P(X'=5)+P(X=5)*P(X'=1) + P(X=2)*P(X'=4)+P(X=4)*P(X'=2) + ...

[mrif]

Pour commencer il faut d'abord définir l'espace de probabilité.
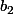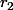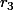Soient et les 2 boules blanches, et les 2 boules rouges, 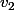,,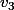, 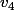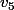les 4 boules vertes.

Si on note l'ensemble de toutes les boules, .
Comme il y a remise, l'espace de probabilité est .


a) Soit alors et

b) Soit alors
et

c) tu commences par trouver la probabilité d'avoir 2 boules rouges en utilisant le meme procédé qu'en a) et b), et ensuite tu utilises le complémentaire de C, ce qui donnera

d) Tu énumères tous les couples qui vérifient la condition.
Sauf erreur tu trouveras

e) meme procédé qu'en d)

f) Si on note l'ensemble des boules impaires, , alors et

[Mehdilis]

Pour commencer il faut d'abord définir l'espace de probabilité.
Soient et les 2 boules blanches, et les 2 boules rouges, ,,, les 4 boules vertes.

Si on note l'ensemble de toutes les boules, .
Comme il y a remise, l'espace de probabilité est .


a) Soit alors et

b) Soit alors
et

c) tu commences par trouver la probabilité d'avoir 2 boules rouges en utilisant le meme procédé qu'en a) et b), et ensuite tu utilises le complémentaire de C, ce qui donnera

d) Tu énumères tous les couples qui vérifient la condition.
Sauf erreur tu trouveras

e) meme procédé qu'en d)

f) Si on note l'ensemble des boules impaires, , alors et

Un grand merci pour ton aide