Bonjour,
J'ai cet exercice de transformation de plan en algèbre linéaire que je n'arrive pas à réussir, voici l'énnoncé et les réponses:
Faire effectuer au triangle A (2,1) ; B(1,2) ; C(2,2) une symétrie orthogonale par rapport à la droite y = 2x + 1
(méthode matricielle + calcul)
A(-1.2,2.6) ; B(0.2,2.4) ; C(-0.4,3.2)
J'aurai besoin que quelqu'un le résolve étapes par étapes pour que je comprenne comment m'y prendre.
Merci
Exercice dalgèbre linéaire
5 messages
- Page 1 sur 1
Duffman1 a écrit:Bonjour,
J'ai cet exercice de transformation de plan en algèbre linéaire que je n'arrive pas à réussir, voici l'énnoncé et les réponses:
Faire effectuer au triangle A (2,1) ; B(1,2) ; C(2,2) une symétrie orthogonale par rapport à la droite y = 2x + 1
(méthode matricielle + calcul)
A(-1.2,2.6) ; B(0.2,2.4) ; C(-0.4,3.2)
J'aurai besoin que quelqu'un le résolve étapes par étapes pour que je comprenne comment m'y prendre.
Merci
salut
Pourquoi pas un changement de repère
(O',I,J)
avec O'(0;1) et les vecteurs: I=(1;2) et J(-2,1)
on a x=X-2Y
et y=2X+Y+1
Pour B:
si (x,y)=(1,2)
X=3/5 et Y=-1/5
X'=X et Y'=-Y
x'=3/5-2/5=1/5=0,2
y'=-2/5+1/5+1=12/5=2,4
B'(0,2;2,4)
Salut,
Une méthode dont les calculs sont au fond totalement identiques mais présenté de manière légèrement différents :
Si tu as une droite D passant par et dirigée par
et dirigée par  alors l'image
alors l'image 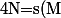) d'un point
d'un point 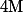 par la symétrie doit être tel que :
par la symétrie doit être tel que :
(1) Le milieu I de [MN] est sur la droite D donc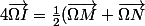=\lambda \vec{u}) avec
avec 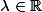
(2) doit être orthogonal à
doit être orthogonal à  donc
donc  (produit scalaire)
(produit scalaire)
Le (1) te donne puis le (2) donne
puis le (2) donne  donc
donc 
Conclusion :=\Omega-\vec{\Omega M} +2\frac{\langle\vec{\Omega M}|\vec{u}\rangle}{||\vec{u}||^2} \vec{u})
A.N. : Si) ;
; ) ;
; ) alors
alors \ :\ (0,1)-(x,y-1)+2\frac{x+2(y-1)}{1^1+2^2}(1,2)\ <br />=\ \big(\frac{-3x+4y-4}{5}\,,\,\frac{4x+3y+2}{5}\big))
Une méthode dont les calculs sont au fond totalement identiques mais présenté de manière légèrement différents :
Si tu as une droite D passant par
(1) Le milieu I de [MN] est sur la droite D donc
(2)
Le (1) te donne
Conclusion :
A.N. : Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
