Etudier la continuité d'une fonction selon lambda

[Pix]

Bonjour à tous,

J'ai une question où la réponse succincte ne me dit pas grand chose. Pourriez-vous m'aider ?

Merci d'avance,

On demande d'étudier la continuité de la fonction suivante suivant la valeur de lambda :



En solution, on dit que la fonction est continue dans R si lambda vaut -1 et qu'elle est continue dans R sauf 1 pour toute autre valeur de lambda.

En dessinant le graphe de ces deux fonctions quand lambda vaut -1, je vois que la fonction est continue mais je ne comprends pas comment on en est arrivé là.

Merci !

[LB2]

Plus simplement, il s'agit de déterminer la valeur de qui va donner le bon "raccord" de cette fonction de x en x=1

On obtient l'équation d'où

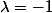
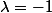
Le choix de te donne donc une fonction continue sur R.
Tout autre choix entraine une discontinuité en x = 1 (par unicité de la limite)

[Pix]

Parfait, merci. Très clair et compréhensible.