Etude d'une suite d'intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 23 Mai 2015, 14:09
par jonses » 23 Mai 2015, 14:09
Bonjour,
J'essaye de faire un petit exercice traitant des suites d'intégrale. Mais ça fait un moment que je bloque, du coup j'aurai bien besoin d'un coup de pouce svp.
---
Je dois prouver l'existence de
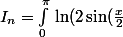)\cos(nx)\, \mathrm dx)
et je dois déterminer sa limite quand n tend vers l'infini
---
J'ai déjà établi l'existence, mais je n'arrive pas à déterminer la limite de cette intégrale.
Si quelqu'un peut m'aider svp.
Je vous remercie d'avance pour vos réponses.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Mai 2015, 14:49
par Ben314 » 23 Mai 2015, 14:49
Salut,
Perso, avant même de commencer à réfléchir, je ferais une i.p.p. pour virer le log (en justifiant bien sûr que c'est licite)
Ensuite, ça dépend pas mal de ton bagage vu qu'on tombe sur un truc assez "standard" dans le domaine des séries de Fourrier et/ou des intégrales calculables par la méthode des résidus.
Si tu connait un de ces domaines, ça peut servir, sinon, un procédé "classique" concernant le type d'intégrale que tu vas obtenir est de les couper en deux de 0 à an puis de an à pi avec un an "bien choisi" (qui va évidement tendre vers 0) de façon à pouvoir majorer/minorer efficacement les sin(?) [pour ? proche de 0 on majore sin(?)
Bon courage...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Axiom
- Membre Naturel
- Messages: 82
- Enregistré le: 22 Mai 2015, 20:10
-
 par Axiom » 23 Mai 2015, 22:13
par Axiom » 23 Mai 2015, 22:13
Bonsoir Jones,
Tu peux faire un changement de variable en posant

Il s'ensuit que :
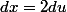
et, si

si

On obtient
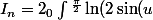) \cos(2nu) du)
On enchaine avec une IPP en posant :
)\rightarrow v'=\cot(u))
et
\rightarrow w=\frac{\sin(2nu)}{2n})
Après simplification,
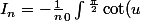\sin(2nu) du)
Je sais pas si ça fait avancer le schmilblick, mais bon... ^^'
Je pense que le mieux est de passer par des séries de Fourier comme le proposait Ben314.. :lol3:
Bon courage également.. :ptdr:
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 25 Mai 2015, 14:16
par jonses » 25 Mai 2015, 14:16
Merci pour vous réponses. (J'ai pas pu répondre plus tôt)
Je n'ai pas vu la méthode des résidus pour calculer les intégrales, et les séries de Fourier ne sont plus au programme de prépa.
Mais, je me suis demandé si on pouvait pas utiliser le lemme de Riemann-Lebesgue ici ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Mai 2015, 15:10
par Ben314 » 25 Mai 2015, 15:10
Y'a le
Théorème de Riemann-Lebesgue alors qu'y a pas les séries de Fourier au programme !!!!
Ca explique mieux pourquoi pour tant d'étudiants, les maths c'est des "formules à appliquer" auquel on comprend que dalle :mur:
Donc oui, tu peut évidement utiliser ce résultat (qui fait parti intégrante de la théorie des séries de Fourier...) et il te reste uniquement à montrer que la fonction x->ln(2*sin(x/2)) est bien intégrable sur [0,pi] (si l'énoncé qu'on vous donne du théorème de Riemann-Lebesgue est le bon : je me méfie...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 25 Mai 2015, 15:15
par Doraki » 25 Mai 2015, 15:15
jonses a écrit:et les séries de Fourier ne sont plus au programme de prépa.
:doh: :doh: :doh: :doh: :doh: :doh:
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 25 Mai 2015, 18:45
par jonses » 25 Mai 2015, 18:45
Ben314 a écrit:Y'a le
Théorème de Riemann-Lebesgue alors qu'y a pas les séries de Fourier au programme !!!!
Ca explique mieux pourquoi pour tant d'étudiants, les maths c'est des "formules à appliquer" auquel on comprend que dalle :mur:
Ah non ! C'est pas du tout au programme le lemme de Riemann Lesbegue ! Mais on l'a vu (et revu de nombreuses fois) en exo.
On a vu dans le cas d'une fonction continue par morceau sur un segment, et dans le cas d'une fonction continue par morceau et intégrable sur un intervalle de R
Ben314 a écrit:Donc oui, tu peut évidement utiliser ce résultat (qui fait parti intégrante de la théorie des séries de Fourier...) et il te reste uniquement à montrer que la fonction x->ln(2*sin(x/2)) est bien intégrable sur [0,pi] (si l'énoncé qu'on vous donne du théorème de Riemann-Lebesgue est le bon : je me méfie...)
L'énoncé qu'on a vu c'est exactement le tout premier énoncé de la "version réelle " de
Théorème de Riemann-Lebesgue Ben314 a écrit:y a pas les séries de Fourier au programme !!!!
Ca explique mieux pourquoi pour tant d'étudiants, les maths c'est des "formules à appliquer" auquel on comprend que dalle :mur:
Avec les nouveaux programmes en prépa, beaucoup de choses ont été enlevées (équa diff non linéaire, séries de fourier, courbes paramétrées, intégrale double....) et notre prof de math ne comprend pas du tout la cohérence des programmes

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Mai 2015, 19:38
par zygomatique » 25 Mai 2015, 19:38
salut
il semble évident de ne plus faire grand chose en prépa ... quand on fait moins que rien en lycée ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Mai 2015, 20:38
par Ben314 » 25 Mai 2015, 20:38
jonses a écrit:On a vu dans le cas d'une fonction continue par morceau sur un segment, et dans le cas d'une fonction continue par morceau et intégrable sur un intervalle de R.
L'énoncé qu'on a vu c'est exactement le tout premier énoncé de la "version réelle " de
Théorème de Riemann-Lebesgue
Fait gaffe que, si vous n'avez vu le théorème que dans le cas de fonction "continues par morceaux" (et c'est un peu ce que je craignais), vu la définition usuelle de "continue par morceaux", ici, tu est pas "dans les clous" vu que x->ln(2*sin(x/2)) tend vers l'infini lorsque x->0+.
Enfin, bref, vérifie plutôt 2 fois qu'une que l'énoncé que tu as du théorème peut s'appliquer ici (le premier énoncé de wiki ne suppose pas que f est continue par morceaux, mais uniquement qu'elle est intégrable sur [a,b])
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 25 Mai 2015, 23:49
par jonses » 25 Mai 2015, 23:49
C'est pas ce que j'ai dit ? On a vu le lemme de Riemann pour le cas d' une fonction continue par morceaux, et intégrable sur l'intervalle considéré.
Par exemple pour cet exo en particulier, la fonction x -> ln(2sin(x/2)) est continue par morceaux sur ]0,pi,] et intégrable sur ]0,pi]

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Mai 2015, 12:05
par Ben314 » 26 Mai 2015, 12:05
jonses a écrit:Par exemple pour cet exo en particulier, la fonction x -> ln(2sin(x/2)) est continue par morceaux sur ]0,pi,] et intégrable sur ]0,pi]
Ah....
Ben ça veut dire qu'on a pas la même définition de
continue par morceaux.
Celle que j'utilise en général est celle de Wiki, et avec cette définition là, ln(2sin(x/2)) n'est pas continue par morceaux.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 26 Mai 2015, 15:00
par paquito » 26 Mai 2015, 15:00
Commence par calculer
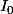
. Après tu intègres par parties et si je me suis pas gouré, tu obtiens :
sin(nx)] entre 0 et \pi -\bigint_{0}^{\pi}\frac{1}{n} \frac{cos(x/2)}{2sin(x/2)} sin(nx)dx)
;
ensuite au voisinage de 0,
)
est équivalent à

et
)
à
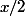
, pour le premier terme, ça s'arrange en 0 et il n'y a aucun problème en

Pour l'intégrale,
}{2sin(x/2)} sin(nx)dx)
doit être équivalent à cos(x/2) au voisinage de 0;
après tu demandes à Ben car j'ai un truc à faire; vérifie les calculs car j'ai fais ça un peu trop vite.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
