Etude d'une suite a laide d'une autre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 14 Déc 2014, 10:14
par adamNIDO » 14 Déc 2014, 10:14
Bonjour,

Pour $S_n$ est une serie geometrique donc
^{k} =\left(\dfrac{1}{3}\right)^{0}. \dfrac{1-\left(\dfrac{1}{3}\right)^{n+1}}{1-\left(\dfrac{1}{3}\right)}=\dfrac{3}{2}( 1-\left(\dfrac{1}{3}\right)^{n+1} ))
Quand

voila une methode mais si possible s'il ya dautre merci
=\sum_{k=0}^\infty x^k)
or
)
est une suite geometrique alors on a $
=\frac1{1-x},\quad |x|<1)
Donc
=\sum_{k=0}^\infty k x^{k-1}=\frac1{(1-x)^2})
En particulier pour

on obtient
^2}=\frac34)
merci pour votre aide
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 14 Déc 2014, 10:41
par Joker62 » 14 Déc 2014, 10:41
Hello,
Étudie S_n(x) = sum(k=0^n) x^k
On a S_n = S_n(1/3)
Dérive x--->S_n(x) pour voir.
-
zaidoun
- Membre Relatif
- Messages: 179
- Enregistré le: 27 Juil 2013, 16:41
-
 par zaidoun » 14 Déc 2014, 10:50
par zaidoun » 14 Déc 2014, 10:50
Bonjour,

Après un petit calcul, tu trouves que
)
D'où
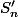
converge vers 3/4
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 14 Déc 2014, 10:59
par adamNIDO » 14 Déc 2014, 10:59
zaidoun a écrit:Bonjour,

Après un petit calcul, tu trouves que
)
D'où
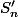
converge vers 3/4
voila c'est une autre methode que celle ci
=\sum_{k=0}^\infty x^k)
or
)
est une suite geometrique alors on a $
=\frac1{1-x},\quad |x|<1)
Donc
=\sum_{k=0}^\infty k x^{k-1}=\frac1{(1-x)^2})
En particulier pour

on obtient
^2}=\frac34)
pouvez vous detaille votre methode un petit peu
-
zaidoun
- Membre Relatif
- Messages: 179
- Enregistré le: 27 Juil 2013, 16:41
-
 par zaidoun » 14 Déc 2014, 11:10
par zaidoun » 14 Déc 2014, 11:10
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 14 Déc 2014, 11:32
par adamNIDO » 14 Déc 2014, 11:32
zaidoun a écrit:
=


(remarquer que

)
oui je vois merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités

