Etude de la fonction exp(x)cos(x)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
gillou87
- Messages: 6
- Enregistré le: 08 Juil 2009, 09:36
-
 par gillou87 » 08 Juil 2009, 09:43
par gillou87 » 08 Juil 2009, 09:43
Salut à tous !
C'est mon premier post sur le forum, j'espère pouvoir y trouver l'aide nécessaire à mon petit problème !
Voilà la bête :
)
Et mon soucis est d'étudier les bornes et variations de cette fonction
Et même problème pour la dérivée :
-sin(x)))
Je pense qu'il faut changer l'écriture de cette dernière à l'aide des expressions trigo déjà connues mais je galère ....
Merci à tous !
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 08 Juil 2009, 09:50
par girdav » 08 Juil 2009, 09:50
Bonjour.
La bête n'est pas bornée: prenons les
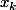
tels que

.
Alors
 = e^{x_k}\cos x_k =\ldots)
et si on prend
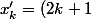 \pi)
on a des trucs intéressants.
Pour les variations regarde sur le cercle trigo quand est-ce que le sinus est plus grand que le cosinus.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 08 Juil 2009, 09:53
par girdav » 08 Juil 2009, 09:53
J'ajoute que ma dernière phrase permet d'étudier les variation sur tout intervalle de la forme
 pi\right])
.
-
gillou87
- Messages: 6
- Enregistré le: 08 Juil 2009, 09:36
-
 par gillou87 » 08 Juil 2009, 10:01
par gillou87 » 08 Juil 2009, 10:01
Merci pour ta réponse !
Mais je ne vois absolument pas comment faire ...
Je n'ai jamais vu ce type de résolution en fait !
Je vais quand même essayé de m'y mettre !
Merci
-
Black Jack
 par Black Jack » 08 Juil 2009, 11:37
par Black Jack » 08 Juil 2009, 11:37
f(x) = e^x * cos(x)
f '(x) = e^x * (cos(x) - sin(x))
f '(x) = V2 * e^x * cos(x + (Pi/4))
Et donc f '(x) a le signe de cos(x + (Pi/4))
...
:zen:
-
gillou87
- Messages: 6
- Enregistré le: 08 Juil 2009, 09:36
-
 par gillou87 » 08 Juil 2009, 12:09
par gillou87 » 08 Juil 2009, 12:09
Donc sa voudrait dire que

Car

Et
 = 0)
Et donc pour encadrer x :
La fonction est négative pour

Est ce juste ??
-
tigre
- Membre Relatif
- Messages: 176
- Enregistré le: 02 Oct 2008, 18:09
-
 par tigre » 08 Juil 2009, 12:19
par tigre » 08 Juil 2009, 12:19
gillou87 a écrit:Salut à tous !
C'est mon premier post sur le forum, j'espère pouvoir y trouver l'aide nécessaire à mon petit problème !
Voilà la bête :
)
Et mon soucis est d'étudier les bornes et variations de cette fonction
Et même problème pour la dérivée :
-sin(x)))
Je pense qu'il faut changer l'écriture de cette dernière à l'aide des expressions trigo déjà connues mais je galère ....
Merci à tous !
bingo trouve :id:

est toujours positive donc le singe de f`(x) dépend de cos(x)-sin(x)
on étudie cos(x)-sin(x)1
mtn tu peux faire le tableau de variation
mais le problème ces les limites
-
gillou87
- Messages: 6
- Enregistré le: 08 Juil 2009, 09:36
-
 par gillou87 » 08 Juil 2009, 12:25
par gillou87 » 08 Juil 2009, 12:25
C'est justement sa mon problème parce que je ne suis pas habitué à manipuler les fonctions trigo !!
Mais t'es sur que cos(x) - sin(x) = tan(x) ?
-
tigre
- Membre Relatif
- Messages: 176
- Enregistré le: 02 Oct 2008, 18:09
-
 par tigre » 08 Juil 2009, 12:29
par tigre » 08 Juil 2009, 12:29
gillou87 a écrit:C'est justement sa mon problème parce que je ne suis pas habitué à manipuler les fonctions trigo !!
Mais t'es sur que cos(x) - sin(x) = tan(x) ?
tu veux qu`on me tue pour connerie(dsl j`ai soute des étapes)
ok regarde cos(x) - sin(x)1 :id: cette fonction

n`admet pas de limite
-
gillou87
- Messages: 6
- Enregistré le: 08 Juil 2009, 09:36
-
 par gillou87 » 08 Juil 2009, 12:36
par gillou87 » 08 Juil 2009, 12:36
Merci dsl !
En fait j'ai rien compris ! lol
je vois pas le rapport entre cos x < sin x et tan x > 1
-
tigre
- Membre Relatif
- Messages: 176
- Enregistré le: 02 Oct 2008, 18:09
-
 par tigre » 08 Juil 2009, 12:40
par tigre » 08 Juil 2009, 12:40
tigre a écrit:tu veux qu`on me tue pour connerie(dsl j`ai soute des étapes)
ok regarde cos(x) - sin(x)1 :id: cette fonction

n`admet pas de limite
par la suite on a que cette fonction admet une extremum en pi/4+kpi
on étudie la fonction sur 0 2pi puis le reste sera effectuer par une translation
-
tigre
- Membre Relatif
- Messages: 176
- Enregistré le: 02 Oct 2008, 18:09
-
 par tigre » 08 Juil 2009, 12:55
par tigre » 08 Juil 2009, 12:55
gillou87 a écrit:Merci dsl !
En fait j'ai rien compris ! lol
je vois pas le rapport entre cos x 1
ok a>b on peut dire a/b>1 si b diff de 0 :id: la dérivabilité en pi/2 doit être étudier tout seul
-
gillou87
- Messages: 6
- Enregistré le: 08 Juil 2009, 09:36
-
 par gillou87 » 08 Juil 2009, 14:30
par gillou87 » 08 Juil 2009, 14:30
tigre a écrit:ok a>b on peut dire a/b>1 si b diff de 0 :id: la dérivabilité en pi/2 doit être étudier tout seul
Merci ! je viens de comprendre c'était tout con !!
Et donc maintenant que j'ai ces infos je peux normalement étudier le signe de la dérivée !
Mais je ne sais pas comment encadrer la fonction tan (x) ...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Juil 2009, 16:53
par Ericovitchi » 08 Juil 2009, 16:53
je vois pas le rapport entre cos x 1
Effectivement il y a du boulot :doh:

Une inégalité se manie comme une égalité. Pour la première étape j'ai divisé à gauche et à droite par cos x et pour la seconde la définition de la tangente c'est d'être la fonction sin divisée par la fonction cos.
Rien de très mystérieux là-dedans.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Juil 2009, 17:25
par Ericovitchi » 08 Juil 2009, 17:25
la fonction tangente est toujours croissante (entre -pi/2 et pi/2, après le motif se répète). Elle vaut 1 pour pi/4 donc il n'est pas très difficile de voir quand est-ce qu'elle est supérieure à 1.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
