Bonjour à tous
Svp les amis, je ne comprend pas comment l'on restreint l'intervalle de définition d'une courbe paramétrée.
Par exemple, quand on a x(t)=3cost et y(t)=sint
Est ce que le fait que sint et cos t soient toutes deux périodiques de période 2π peut nous aider ?
Merci d'avance
Etude des courbes paramétrées
5 messages
- Page 1 sur 1
Re: Etude des courbes paramétrées
Les deux applications paramètres sont de périodicité  . Donc pour
. Donc pour  on obtient exactement le même point :
on obtient exactement le même point : ,y(t))=(x(t+2\pi),y(t+2\pi)))
La restriction de l'intervalle d'étude (et pas de définition), est utilisée pour simplifier l'étude car au-delà de cet intervalle le comportement de la courbe se déduit du comportement sur cet intervalle.
J'insiste sur "et pas de définition" : par exemple, si on cherche à calculer la longueur du chemin parcouru sur cette courbe entre 0 et t, cette longueur n'est pas du tout périodique
La restriction de l'intervalle d'étude (et pas de définition), est utilisée pour simplifier l'étude car au-delà de cet intervalle le comportement de la courbe se déduit du comportement sur cet intervalle.
J'insiste sur "et pas de définition" : par exemple, si on cherche à calculer la longueur du chemin parcouru sur cette courbe entre 0 et t, cette longueur n'est pas du tout périodique
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Etude des courbes paramétrées
Ok mais quelle incidence pourrait avoir le fait que (x(t), y(t))=(x(t+2π), y(t+2π)) peut il avoir sur l'intervalle de définition ?
Re: Etude des courbes paramétrées
Je ne comprends pas la question. "Intervalle de définition" n'est pas une notion standard : on parle de "domaine de définition" pour exprimer le plus grand sous-ensemble sur lequel la fonction est une application (tout élément admet une image).
Ici, la fonction est : définie par
définie par =\Big(3\cos(t),sin(t)\Big)) , le domaine de définition est donc
, le domaine de définition est donc  puisque tout réel admet bien une image.
puisque tout réel admet bien une image.
Le fait que la fonction soit périodique n'y change rien.
Par contre pour étudier une fonction périodique de période , il suffit de l'étudier sur un intervalle dont la longueur est une période : comme
, il suffit de l'étudier sur un intervalle dont la longueur est une période : comme =f(x)) pour tout x, ce qui se passe sur
pour tout x, ce qui se passe sur  est semblable à ce qui se passe sur
est semblable à ce qui se passe sur  , et semblable à ce qui se passe sur
, et semblable à ce qui se passe sur T[) : continuité, dérivabilité, sens de variation, signe...
: continuité, dérivabilité, sens de variation, signe...
Or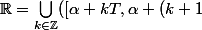T[) , c'est même une partition, on a donc couvert l'ensemble du domaine de définition, il y a juste à s'assurer de ce qui se passe aux points de jonctions : donc en
, c'est même une partition, on a donc couvert l'ensemble du domaine de définition, il y a juste à s'assurer de ce qui se passe aux points de jonctions : donc en  (continuité à gauche, dérivabilité à gauche...)
(continuité à gauche, dérivabilité à gauche...)
Le choix de dépend du contexte ; par exemple, s'il y a des symétries par rapport à l'origine, on prendra l'intervalle
dépend du contexte ; par exemple, s'il y a des symétries par rapport à l'origine, on prendra l'intervalle  , mais ce n'est pas une obligation.
, mais ce n'est pas une obligation.
Ici, la fonction est :
Le fait que la fonction soit périodique n'y change rien.
Par contre pour étudier une fonction périodique de période
Or
Le choix de
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
