Bonsoir,
J'ai besoin de votre aide pour m'aider à interpréter certains résultats que je ne parviens pas très bien à démontrer.
EnoncéLa normale principale d'une courbe birégulière
dans
au point
)
est la droite dirigée par la normale à
et passant par
.
Pour une courbe
birégulière, on note (T,N,B) son repère de Frénet. La courbe paramétrée lisse birégulière
est une
courbe de Bertrand : c'est à dire qu'il existe une autre courbe lisse
avec les mêmes normales principales. On suppose que
(mais pas
) est paramétrée par longueur d'arc. On a donc :
 = \epsilon N_{\alpha}(s))
qui sont paralèlles au vecteur
\beta(s)})
et où
= +1 ou -1
Question 1Montrer que
 = \alpha(s) + rN_{\alpha}(s))
où (
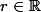
)est constant
Question 2Montrer qur l'angle
entre les vecteurs tangents
et
est constant (On pourra considérer
. On remarquera que le signe de
est arbitraire.
Question 3Montrer que
)
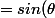(quitte à changer le signe de
) et montrer que
)
Question 4En déduire qu'il existe 2 constantes réelles a et b telles que :
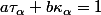
(On pourra considérer
où
et
sont la torsion et la courbure de la courbe
Pour la 1ère question je peux peut-être dériver l'expression et utiliser les formules de Frénet mais je n'aboutis pas... sinon je peux tjrs écrire que
\beta(s)} = rN_{\alpha}(s))
Pour la 2ème question il faut dériver le produit scalaire je pense (?)
Pour les questions 3 et 4 je suis bloqué...
D'une manière générale j'ai essayé de représenter géométriquement ces 2 courbes alpha et beta ayant les mêmes normales principales, cependant je n'ai pas toujours les conditions
qui sont paralèlles au vecteur
et où
= +1 ou -1. Je ne sais pas comment représenter tout ça. Bref, j'ai vraiment besoin de votre aide sans quoi je sens que je ne vais pas avancer.
Merci à vous!
