Espérance conditionnelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gorosei
- Membre Naturel
- Messages: 42
- Enregistré le: 09 Juin 2018, 17:05
-
 par Gorosei » 24 Juin 2019, 18:13
par Gorosei » 24 Juin 2019, 18:13
Bonjour,
Soit X,Y deux variables aléatoire indépendantes uniformément distribués sur [0,3] et soit
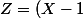^2)
1) Calculer E[X|Z]
2) Calculer E[Z|X]
3) Calculer E[Y|Z]
4) Prouver que pour toute fonction f mesurable bornée :
|Y,Z]=E[f(X)|Z])
2)
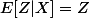
3)
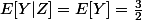
Pouvez vous m'aider pour la 1 et 4 svp.
Merci
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 24 Juin 2019, 18:21
par LB2 » 24 Juin 2019, 18:21
Pour la 4, il faut utiliser l'indépendance de X et Y.
Pour la 1. , tu peux utiliser des densités
-
Gorosei
- Membre Naturel
- Messages: 42
- Enregistré le: 09 Juin 2018, 17:05
-
 par Gorosei » 24 Juin 2019, 19:05
par Gorosei » 24 Juin 2019, 19:05
1)
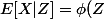 \\ \forall \psi(Z) \ E[\psi (Z)(X-\phi(Z))]=0 \\ E[\psi (X^2-2X+1)(X-\phi(X^2-2X+1))]=0 \\ \int_{0}^{3}{\psi (X^2-2X+1)(X-\phi(X^2-2X+1)) \frac{dx}{3}=0})
chgt de variable:
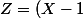^2, \ X=\sqrt{Z}+1 ,\ dx=\frac{dz}{2 \sqrt{z}})
(\sqrt{Z}+1-\phi(Z)) \frac{dz}{6\sqrt{z}}=0})
=\sqrt{Z}+1)
et donc
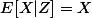
Est-ce juste ?
-
Gorosei
- Membre Naturel
- Messages: 42
- Enregistré le: 09 Juin 2018, 17:05
-
 par Gorosei » 24 Juin 2019, 19:30
par Gorosei » 24 Juin 2019, 19:30
4) si X et Y sont indépendants, alors
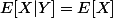
mais je ne vois pas comment l'utiliser avec la fonction.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 24 Juin 2019, 19:56
par LB2 » 24 Juin 2019, 19:56
si tu ne vois pas, repasse par des densités et utilise l'indépendance
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 24 Juin 2019, 19:57
par LB2 » 24 Juin 2019, 19:57
Gorosei a écrit:1)
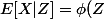 \\ \forall \psi(Z) \ E[\psi (Z)(X-\phi(Z))]=0 \\ E[\psi (X^2-2X+1)(X-\phi(X^2-2X+1))]=0 \\ \int_{0}^{3}{\psi (X^2-2X+1)(X-\phi(X^2-2X+1)) \frac{dx}{3}=0})
chgt de variable:
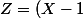^2, \ X=\sqrt{Z}+1 ,\ dx=\frac{dz}{2 \sqrt{z}})
(\sqrt{Z}+1-\phi(Z)) \frac{dz}{6\sqrt{z}}=0})
=\sqrt{Z}+1)
et donc
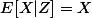
Est-ce juste ?
je pense qu'il y a un problème avec ton changement de variable qui n'est pas bijectif (X-1 n'a pas de raison d'être positif a priori)
-
Gorosei
- Membre Naturel
- Messages: 42
- Enregistré le: 09 Juin 2018, 17:05
-
 par Gorosei » 24 Juin 2019, 20:31
par Gorosei » 24 Juin 2019, 20:31
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 24 Juin 2019, 22:41
par LB2 » 24 Juin 2019, 22:41
EDIT : Bêtise, voir le post de GBZM
Modifié en dernier par
LB2 le 25 Juin 2019, 10:12, modifié 1 fois.
-
Gorosei
- Membre Naturel
- Messages: 42
- Enregistré le: 09 Juin 2018, 17:05
-
 par Gorosei » 25 Juin 2019, 00:12
par Gorosei » 25 Juin 2019, 00:12
Je prends alors
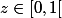
?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 25 Juin 2019, 09:59
par GaBuZoMeu » 25 Juin 2019, 09:59
Intuitivement, il est clair que l'espérance de

sachant que
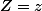
est :

si
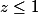
(les deux valeurs
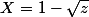
et
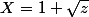
sont équiprobables)
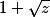
si
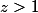
.
Il n'y a pas de "raccord" en
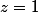
.
Il n'y a plus qu'à confirmer cette intuition (juste) par un calcul.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
