Espace stable algèbre lineaire

[elvis77]

Bonjour à tous,

Voici mon problème, je suis dans un exercice où on cause de transposée, jusque là pas de souci, je découvre les différentes propriétés de la transposée.
Un question arrive : PHI une forme linéaire, H = Ker (PHI) on suppose que H stable par f ( f appartient à L(E)).
Montrer qu'il existe a appartenant a E tq PHI(a)=1.
J'ai travaillé avec le fait que H stable par f, que H hyperplan donc tout element de X s'écrit comme x = x1+alpha.v avec x1 dans H et v pas dans H et alpha dans K. Puis j'ai bidouillé tout ça sans rien obtenir.
Après j'ai trouvé une assetion qui dit : f(H) inclu dans H <=> il existe lambda dans K tq f=lambda.Id, j'ai rebidouillé tout ça avec le reste et j'arrive pas a montrer ce que je veux.

Si quelqu'un a une idée, une piste, je suis preneur, ça fait pas mal de temps que je me prends la tête la dessus.

Merci d'avance

Bien cordialement

Elvis.

[alavacommejetepousse]

bonjour
je présume que phi est non nulle (sinon imposible)

phi étant non nulle il existe v tel que phi (v) non nul

et on prend a = v / ph(i)

[elvis77]

Merci pour votre réponse mais je ne comprend pas pourquoi choisir a=v/ph(i), je suppose que vous vouliez mettre a=v/PHI(v). Outrepassé cette faute de frappe je pense avoir compris. Ensuite on compose par PHI et on obtient bien PHI(a)=1.
Merci "alavacommejetepousse"
PS : en effet on suppose PHI non nulle

[Nightmare]

Salut,

je ne comprends pas l'utilité de f, ce a existe toujours : à coeff multiplicatif,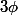 est, à un scalaire multiplicatif près, l'application 2ème coordonnée où E est décomposé en avec .

Autrement dit, soit x dans E,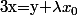 . On pose alors la forme linéaire qui envoie x sur lambda. Elle est de noyau H donc homothétique à 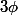. Je te laisse examiner la valeur en x0 !

[elvis77]

Merci de votre réponse, j'aimerai avoir plus d'éclairage concernant certains points : tout d'abord, f ne sert à rien c'est dans les questions précédentes de l'exo qu'il nous sert.

concernant la valeur en x0 : PSY(x0)=PSY(1/lambda*(x-y)) heum... attends....je viens de refaire mon calcul j'avais oublié que PSY était définit comme une forme linéaire donc ça marche par contre je ne pouvais pas le deviner car on ne fonctionne pas comme ça ("homothétique" je sais pas ce que ça veut dire)

merci bien pour cette autre solution

bien cordialement

Elvis

[elvis77]

ah si une derniere chose, on a PSY(x0)=1 et comme PSY est homothétique à PHI on peut dire que PHI(x0)=1 je me trompe ou c'est bien cela ?
Merci

[Nightmare]

Cela voulait dire que avec alpha un certain scalaire