Equivalence de suites

[barbu23]

Bonsoir à tous, :happy3:

Est ce que, à l'infini, si et alors, ?

Merci d'avance. :happy3:

[Luc]

Bonsoir à tous, :happy3:

Est ce que, à l'infini, si et alors, ?

Merci d'avance. :happy3:

Oui dans le cas où elles ne sont pas stationnaires en 0, car



Dans le cas où g (resp. h) stationne en 0, alors (resp. v) stationne en 0 aussi, donc c'est vrai aussi dans ce cas.

[barbu23]

Par exemple, est ce que : ?

[Luc]

Par exemple, est ce que : ?

Si m est fixé et ne dépend pas de n, oui.

[barbu23]

Est ce que, à l'infini, si et alors, ?
Est ce que, à l'infini, si alors, avec une suite réelle ?
Où est le problème ici :
http://rinconmatematico.com/foros/index.php/topic,61424.msg246138/topicseen.html#msg246138
:hein: :hein: :hein:
Merci d'avance. :happy3:

[Luc]

Sur l'exemple, je ne vois pas ce qui te pose problème.

La limite cherchée vaut + l'infini, si m est supérieur ou égal à 2.

Et 0 si m=1.

Sinon, en général, on ne peut pas additionner les équivalents (à cause du signe a priori non constant)

[barbu23]

Je ne comprends pas bien ça :
.
Comment calculer,
Moi, j'ai dit que : , car :

Et donc :

Correct ? Où est l'erreur ?

[barbu23]

J'ai appliqué ça :

Est ce que, à l'infini, si alors, avec une suite réelle

Mais, pas ça : ( qui est fausse )

Est ce que, à l'infini, si et alors,

[Luc]

J'ai appliqué ça :

Mais, pas ça : ( qui est fausse )

Ok, je vais regarder en détail, mais j'ai quand même un gros doute.

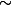
Il faut que tu revoies absolument la notion de qui n'est manifestement pas comprise.

En effet, dans l'exemple, savoir que
te dit que la différence est un , rien de plus. En aucun cas tu ne peux déduire que la différence est nulle.

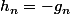
EDIT : Ta première proposition est évidemment fausse, elle aussi. Regarde ce qui ce passe quand . En revanche, si toutes les suites ont le même signe et un signe constant, c'est peut-être vrai.

[barbu23]

Merci beaucoup. :happy3: