
Equivalence de deux suites
6 messages
- Page 1 sur 1
Re: Equivalence de deux suites
Bonjour
En cas de pb (i.e de de doute) comme dans ce cas tu reviens à la définition:
(la ou les fonctions ci-après ont pour limite 0)
ci-après ont pour limite 0)
 signifie
signifie 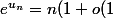)=n(1+\epsilon(n)))
Et puisque) tend vers 0,
tend vers 0, ) est bornée
est bornée
Donc a bien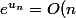.)
D'ailleurs concernant la démo, il vaut mieux faire comme tu as fait.
En cas de pb (i.e de de doute) comme dans ce cas tu reviens à la définition:
(la ou les fonctions
Et puisque
Donc a bien
D'ailleurs concernant la démo, il vaut mieux faire comme tu as fait.
Re: Equivalence de deux suites
pour moi, si on enlève pas le o(n) souligné, les égalité sont fausses
si on remplace o(n) par O(n), c'est faux aussi car la 'constante' n'est pas forcément 1 dans le O(n).
si on remplace o(n) par O(n), c'est faux aussi car la 'constante' n'est pas forcément 1 dans le O(n).
Re: Equivalence de deux suites
Salut
@pascal16 Je ne comprends pas ta remarque. D'abord ce qui est souligné est un grand O mais de plus c'est correct. Il faut revoir la définition de grand O.
@pascal16 Je ne comprends pas ta remarque. D'abord ce qui est souligné est un grand O mais de plus c'est correct. Il faut revoir la définition de grand O.
Re: Equivalence de deux suites
Bonsoir,
il y a une erreur dans la correction, il faut lire e^(u_n)=n+o(n) et pas e^(u_n)=o(n)
Ta solution est meilleure : on pouvait écrire un peu mieux : ln(n)=u_n+o(1) au lieu de ln(n)=u_n+o(u_n)
mais puisque ici on ne cherchait qu'un équivalent simple de u_n, ln(n)=u_n+o(u_n) suffit. Un bon exercice est de calculer le deuxième terme du développement asymptotique de u_n, c'est à dire un équivalent simple de u_n-ln(n)
il y a une erreur dans la correction, il faut lire e^(u_n)=n+o(n) et pas e^(u_n)=o(n)
Ta solution est meilleure : on pouvait écrire un peu mieux : ln(n)=u_n+o(1) au lieu de ln(n)=u_n+o(u_n)
mais puisque ici on ne cherchait qu'un équivalent simple de u_n, ln(n)=u_n+o(u_n) suffit. Un bon exercice est de calculer le deuxième terme du développement asymptotique de u_n, c'est à dire un équivalent simple de u_n-ln(n)
Re: Equivalence de deux suites
dans mes souvenirs, j'avais que la notation "O" est bien moins puissante que "o".
après un wiki rappel :
An=O(n) <=> il existe une constante k positive non nulle telle que |An| < kn ("pour n grand")
donc si c'est un "O" qui est souligné, il n’implique pas la suite de la ligne
et en particulier An=0, An= con(n) marchent toujours
An∼n <=> An=n+o(n) est elle juste
An∼n <=> An=n+O(1) me semble bonne aussi
donc la fin de la ligne est juste et ton explication est juste
après un wiki rappel :
An=O(n) <=> il existe une constante k positive non nulle telle que |An| < kn ("pour n grand")
donc si c'est un "O" qui est souligné, il n’implique pas la suite de la ligne
et en particulier An=0, An= con(n) marchent toujours
An∼n <=> An=n+o(n) est elle juste
An∼n <=> An=n+O(1) me semble bonne aussi
donc la fin de la ligne est juste et ton explication est juste
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
