Bonjour,
Dans une séance de cours, notre professeur nous lâche une petite bombe:

et P(

) ont même puissance au sens de cardinalité. ça m'est paru étrange vu que je me suis plutôt habitué au

topologique "tout puissant" avec sa continuité, complétude, etc... et P(

), bah ça reste des entiers et donc du discret. Bref, disons que ça a été suffisant pour attiser ma curiosité :p.
Dans une première approche, on peut remarquer que chaque réel possède une écriture décimale, soit un ensemble de couples
)
avec

le rang et

chiffre (compris entre 1 et 9). Cependant il y a certaines problèmes qu'il faut surmonter:
1/ Une telle application va vers

x[(1,9)]), il faut donc se débarrasser de

en réduisant l'intervalle de

au minimum: On passe à l'écriture binaire.
2/La non-unicité du développement décimal: il suffit de prendre l'écriture minimale, qui quant à elle est unique.
3/

est relatif: On raisonne sur une intervalle où r est positif vu que

est bijectable avec toute intervalle de

.
Je vais donc raisonner seulement sur l'intervalle [0,1[ vu que

s'y ramène moyennant des inversions.
Soit donc:
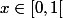

Si

On prend:

Qui n'est autre que l'écriture minimale de

(par analogie: 0,
9=1)
On définit donc notre fonction:


{

}
Cette application est injective:
Pour

et

=f\left(y\right)\,\Rightarrow \,\forall \,i\,\in \,\mathbb{N}\,{a}_{i}=1\,\Longleftrightarrow {b}_{i}=1)
(le principe même d'une base).
Par contre-apposée:

Donc:

Donc:

L'application est aussi surjective:
Pour
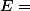
{
})
}
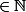
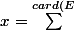}_{k=1}{2}^{{-i}_{k}})
est un antécédent de

.
L'application est donc bel et bien bijective.

et P(

) ont donc même puissance au sens de cardinalité.
Place maintenant aux questions:
1/Le charabia que j'ai écrit est-il compréhensible?
2/Si oui, est-il correct?
3/Puisque

est "un cran" supérieur à

au sens de puissance, est-ce-que on a plus généralement pour tout ensemble infini

,
\right)=ord\left(E\right)+1)
?
4/Peut-on de même exhiber une bijection entre

et
)
, l'ensemble des fonctions continues sur

, parce que

et P(

), ça va un peu, mais de là à réduire toute une fonction en un réel...
Merci d'avance.
