équipotence

par **sue** » 22 Sep 2007, 23:24

bonsoir,

une question du cours:
je veux mq

et équipotent à

,

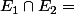
(sans card)

une indication ? merci

par **fahr451** » 22 Sep 2007, 23:26

bonsoir

soit phi : f -> (f l E1 , f l E2)

où f l E1 désigne la restriction de f à E1

phi est une bijection

par **sue** » 22 Sep 2007, 23:35

ah d'accord !

mais comment on construit en général ces bijections , je trouve du mal moi :triste:

par **fahr451** » 22 Sep 2007, 23:38

ben en général on cherche

ici on n 'a pas grand choix

F^(E1U E2) ensemble des applications de F ds E1 U E2

F^E1................................ ............. F dans E1

comment passe t on de l 'une à l'autre

restriction c 'est naturel

par **sue** » 22 Sep 2007, 23:45

Ok , c vrai que c'est évident ici , mais j'imagine que parfois c pas si évident .
peux tu me donner un autre exemple stp ?

par **fahr451** » 22 Sep 2007, 23:50

P ( E) et E^{0,1}

par **kazeriahm** » 22 Sep 2007, 23:53

bonsoir

N et Z, N et Q ?!

par **sue** » 23 Sep 2007, 00:00

dsl prob de connexion !

x -- phi x tq phi la fct caractéristique (bijective) c ça ?

par **fahr451** » 23 Sep 2007, 00:06

oui même genre

E un ensemble fini

A = { (X,Y,Z) avec X C Y C Z C E}
C : lire inclus
et {1,2,3,4}^E

je me rends compte que ds le précédent message j 'aurais du écrire {0,1}^E

(je n'aime pas cette notation)

bonne nuit

par **sue** » 23 Sep 2007, 00:25

@kazeriahm : pr N et Z ok (dans le cours) je ne vois pas pr N et Q .

@fahr: ok je vais voir pr cet ex . bonne nuit

ps: dsl si je tarde pr répondre j'ai des probs de connexion !

par **SimonB** » 23 Sep 2007, 10:14

sue a écrit:@kazeriahm : pr N et Z ok (dans le cours) je ne vois pas pr N et Q .

http://fr.wikipedia.org/wiki/Infini te donne une bijection possible entre N et Q.

Cela dit, un théorème vaut parfois mieux qu'une bijection construite ex nihilo : en l'occurrence, si l'on appelle "dénombrable" le fait pour un ensemble E d'être en bijection avec N (ce qui signifie qu'on peut indexer les éléments de E avec des nombres entiers positifs), on a un joli théorème qui dit qu'une union dénombrable d'ensembles dénombrables est dénombrable. Et on peut appliquer ce résultat à Q.

par **sue** » 23 Sep 2007, 11:12

Bonjour,

merci SinonB pour ces infos je ne savais pas pour la dénombrabilité .

sinon fahr pour le dernier exemple je dirais : (XYZ) --- phi tq phi : E --- {1.2.3.4} x -- { 1 si x £ X , 2 si x £ Y\X , 3 si x£ Z\Y , 4 si x£ E\Z }

non?

par **fahr451** » 23 Sep 2007, 11:14

bravo sue

méthode éfficace par régionnements infiniment plus simple que de discuter suivant les cardinaux respectifs de X,Y,Z et d'utiliser le binôme

par **sue** » 23 Sep 2007, 11:20

merci

sinon une question : si E et F 2 ensembles finis sont équipotents que peut on dire sur P(E) et P(F) le sont également ?
je pense que oui .

par **fahr451** » 23 Sep 2007, 11:22

tu as les cardinaux de ces ensembles ...

mais tu peux retirer le mot fini

par **sue** » 23 Sep 2007, 11:26

peut on parler de cardinal en cas d'ensembles infinis ?

par **fahr451** » 23 Sep 2007, 11:27

si E et F sont équipotents P(E) et P(F) le sont

-cas fini évident
-cas infini facile

par **sue** » 23 Sep 2007, 11:33

sans cardinaux au cas d'infini je ne vois pas

par **sue** » 23 Sep 2007, 11:37

Ah d'accord on peut faire par l'absurde

par **fahr451** » 23 Sep 2007, 11:37

f bijection de E sur F

phi P(E) ->P(F)
X -> phi(X) = f(X)
phi bijective

équipotence

équipotence

Qui est en ligne