Equation 4 inconnus
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 16 Jan 2014, 01:24
par rb90 » 16 Jan 2014, 01:24
Bonsoir
J'ai un souci sur une équation à 4 inconnus, j'ai 3 équations et je dois le faire par Substitution.
y+3z+t=1
x+2y+z+t=2
y-4z=0
Je n'arrive pas à isoler un inconnu...
Comment faire ?
:jap:
-
bneay
- Membre Naturel
- Messages: 53
- Enregistré le: 06 Jan 2014, 23:04
-
 par bneay » 16 Jan 2014, 02:12
par bneay » 16 Jan 2014, 02:12
pivots de gausse, il y a 3 inconnus principaux et 1 secondaire, donc il y aura un paramètre avec lequel les équations s'expriment.. en fin, si l'ensemble des solutions et non nul, il y aura une infinité de solution..
C'est un système linéaire facile à exploiter :lol3:
-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 16 Jan 2014, 02:18
par rb90 » 16 Jan 2014, 02:18
Oue mais gauss c'est pas de la substitution ? c'est de la combinaison !! non ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Jan 2014, 07:52
par chan79 » 16 Jan 2014, 07:52
rb90 a écrit:Oue mais gauss c'est pas de la substitution ? c'est de la combinaison !! non ?
salut
Une méthode parmi d'autres:
En utilisant la première et la troisième égalité, tu exprimes y et z en fonction de t.
Tu substitues ensuite y et z dans la seconde. Tu obtiens x en fonction de t
-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 16 Jan 2014, 11:58
par rb90 » 16 Jan 2014, 11:58
merci beaucoup
-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 16 Jan 2014, 21:03
par rb90 » 16 Jan 2014, 21:03
Comment on passe à cette égalité pour la ligne 1 et 2 au début
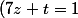 et (x+9z+t=2))
-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 19 Jan 2014, 20:10
par rb90 » 19 Jan 2014, 20:10
En faite c'est le passage de la 2em ligne on a
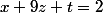
à
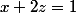
je ne comprend pas le lien.
Merci pour l'aide !
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 19 Jan 2014, 22:08
par aymanemaysae » 19 Jan 2014, 22:08
rb90 a écrit:En faite c'est le passage de la 2em ligne on a
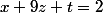
à
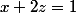
je ne comprend pas le lien.
Merci pour l'aide !
 et (x+9z+t=2) et (y=4z) a (7z+t=1) et (x+2z=2) et (y=4z) })
 par ((x+9z+t)-(7z+t)=2-1) c-a-d x+2z=1 })
-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 19 Jan 2014, 22:57
par rb90 » 19 Jan 2014, 22:57
A partir d'une solution particulière comment vous trouvez rapidement la solution de l'équation
par exemple la premiere avec
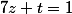
on trouve
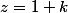
et
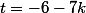
Il y a une technique ?
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 20 Jan 2014, 12:30
par aymanemaysae » 20 Jan 2014, 12:30
rb90 a écrit:A partir d'une solution particulière comment vous trouvez rapidement la solution de l'équation
par exemple la premiere avec
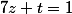
on trouve
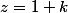
et
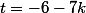
Il y a une technique ?


-
rb90
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Mai 2012, 13:07
-
 par rb90 » 20 Jan 2014, 17:34
par rb90 » 20 Jan 2014, 17:34
Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 333 invités

