Résolution d'UNE équation à 3 inconnus
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lakoumy
- Messages: 7
- Enregistré le: 23 Oct 2008, 16:28
-
 par lakoumy » 03 Nov 2008, 18:14
par lakoumy » 03 Nov 2008, 18:14
bonsoir,
voilà j'ai un problème avec l'équation suivante
10x +15y+6z=1
en observant on remarque que le vecteur de coordonnées (1,-1,1) est solution de l'équation.
ma question c'est comment à partir de ça je peux trouver l'ensemble des solutions de l'équation?
merci
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Nov 2008, 18:34
par yos » 03 Nov 2008, 18:34
Bonsoir.
Tu peux poser u=2x+3y pour te ramener à 5u+6z=1.
-
COTLOD
- Membre Relatif
- Messages: 104
- Enregistré le: 14 Sep 2008, 10:07
-
 par COTLOD » 04 Nov 2008, 12:30
par COTLOD » 04 Nov 2008, 12:30
Bonjours, je crois qu'une methode est de résoudre (comme pour les équation différentielles) l'équation homogène 10x+15y+6z=0, on obtient un espace vectoriel de dimension 2, on ajoute la solution particulière pour obtenir un plan affine.
-
lakoumy
- Messages: 7
- Enregistré le: 23 Oct 2008, 16:28
-
 par lakoumy » 04 Nov 2008, 15:53
par lakoumy » 04 Nov 2008, 15:53
merci COTLOD pour tes informations
j'ai trouvé comme solution Vect{((3/2)y+(3/5)z+1,y-1,z+1),y et z dans Z}
le problème c'est que je dois donner l'ensemble des solutions entières
suffit-il que je détermine les y et z tels que (3/2)y+(3/5)z soit entier?
merci encore
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Nov 2008, 20:56
par yos » 04 Nov 2008, 20:56
COTLOD a écrit:on obtient un espace vectoriel de dimension 2,
C'est plutôt un Z-module et la difficulté est qu'une partie libre à deux éléments n'est pas toujours une base. On peut le faire quand même bien sûr. La méthode que je suggérais plus haut marche très bien aussi. C'est toi qui voit.
-
lakoumy
- Messages: 7
- Enregistré le: 23 Oct 2008, 16:28
-
 par lakoumy » 06 Nov 2008, 16:42
par lakoumy » 06 Nov 2008, 16:42
je n'ai pas trés bien compris ta méthode yos, ni pourquoi poser u=2x+3y
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 06 Nov 2008, 18:50
par yos » 06 Nov 2008, 18:50
Tu sais résoudre ax+by=c dans
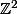
?
Les lignes sont équivalentes entre elles :
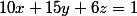
,
+6z=1)
,
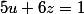
,

,

, et
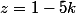
,
\in\mathbb{Z}^2, \, x=3k-3k'+1,\; y=2k'-1,\; z=1-5k)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
