Equation fonctionelle

[cheria2010]

salut tout le monde que dieu vous garde

trouvez toutes les fonction f définies de R vers R tel que :

f(f(x) + x) + x= 3f(x)
et f(0) = 1 .
merci a vous ........

[Ben314]

Salut,
Tu n'aurait pas, par hasard, une quelconque hypothèse de régularité (continuité ? dérivabilité ? intégrabilité ?)

[ffpower]

Sauf que si f est continue, j'obtiens nécessairement que f(0)=0.. ( et à mon avis en poussant un peu il doit n'y avoir que f=Id comme solution )
Et si f n'est pas continue, ya probablement moyen de créer un tas de solutions non explicites, donc ouais, énoncé bizarre..

edit: bon bah j'ai poussé un peu et ya effectivement que f=Id comme solution.

[cheria2010]

Oui bien sur la fonction est continue sur R j'ai oublie ca


mais comment l'identité est une solution alors que f(0) = 1 !

[Ben314]

Oui bien sur la fonction est continue sur R j'ai oublie ca

Sans vouloir "faire le méchant", dans ce type de problème, IL NE FAUT JAMAIS OUBLIER CE TYPE DE CONDITIONS : c'est à peu prés systèmatiquement grâce à elles qu'on peut conclure...

[ffpower]

Oui bien sur la fonction est continue sur R j'ai oublie ca


mais comment l'identité est une solution alors que f(0) = 1 !

Oui, du coup dans ce cas, ya pas de solutions( continues ). L'identité est la seule solution (continue) si on oublie l'hypothese sur f(0)..Et c'est pour ça que je trouve l'exo un peu bizarre.

[Anonyme]

ffpower j'aimerai bien voir comment tu as proceder ..

[ffpower]

Les étapes :
-g(x)=f(x)+x vérifie g o g(x)=4g(x)-4x
-g est injective donc strictement monotone, et même strictement croissante ( en utilisant que g o g est nécessairement croissante )
-g ne peut avoir de limite finie en +-infini, donc g est en fait bijective
-En notant pour n dans Z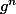 l'itérée n-ieme de g (si n négatif, on itere 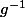), on vérifie que pour tout n de Z, on a avec (se montre en remarquant que la suite est réccurente linéaire d'ordre 2..ou alors en intuitant le résultat puis en faisant une reccurence si on connait pas les suites reccurentes linéaires)
-En utilisant que pour tout n,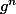 est croissante, et en regardant ce que ca donne quand n tend vers +- l'infini, on doit avoir en fait que est à la fois croissant et décroissant en x, donc constant. Puis on vérifie aisément que cette constante est nulle et donc que f=Id

[cheria2010]

Les étapes :
-g(x)=f(x)+x vérifie g o g(x)=4g(x)-4x
-g est injective donc strictement monotone, et même strictement croissante ( en utilisant que g o g est nécessairement croissante )
-g ne peut avoir de limite finie en +-infini, donc g est en fait bijective
-En notant pour n dans Z l'itérée n-ieme de g (si n négatif, on itere ), on vérifie que pour tout n de Z, on a avec (se montre en remarquant que la suite est réccurente linéaire d'ordre 2..ou alors en intuitant le résultat puis en faisant une reccurence si on connait pas les suites reccurentes linéaires)
-En utilisant que pour tout n, est croissante, et en regardant ce que ca donne quand n tend vers +- l'infini, on doit avoir en fait que est à la fois croissant et décroissant en x, donc constant. Puis on vérifie aisément que cette constante est nulle et donc que f=Id

salut
pardon . j'ai pas compris votre itération
moi je trouve
ou j'ai tort

[Ben314]

Il semblerais qu'effectivement, il y ait une légère faute de frappe.
Il faut lire

......

mais ça ne change rien à la suite...

[ffpower]

ou plutot a(x)=(f(x)-x)/2...coquille effectivement, je corrige :)

PS pour Cheria : pour ton exo initial (ie avec la condition f(0)=1), on peut s'arreter un chouia plus tot dans ma demo : une fois obtenue l'expression de g^n(x), on voit que celle ci tend vers 0 quand n tend vers -infini et donc que nécessairement g(0)=0, ce qui contredit l'hypothese..

PS2 (toujours pour Cheria): sur ce forum, la coutume n'est pas au vouvoiement :++:

PS3 : euh non, pas de PS3 en fait, trop cher pour moi :zen:

[cheria2010]

merci ffpower pour votre travail exemplaire ....