EQUATION FONCTIONELLE

[Napoléon]

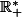
Bonjour, j'ai un problème que je n'arrive pas à résoudre. Soit une fonction définie sur tel que . J'aimerais démontrer que cette fonction est dérivable pour tout . J'ai déjà remarqué que
Il ne me reste donc plus qu'à démontrer la dérivabilité en 1, mais là je ne vois pas du tout comment faire.
Merci beaucoup pour votre aide !

[Napoléon]

Il faut bien sûr rajouter l'hypothèse de continuité de f.

[phyelec]

Bonsoir,

vous pouvez voir si vous aboutissez en prenant g(x)=f(ax) vous avez alors g'(x)=af'(ax) et vous avez également g(x)=f(a)+f(x),
g'(x)=(f(a)+f(x))'=f'(x)=af'(ax) quelque soit a et x de R+

[Napoléon]

Je vois, merci !
Cependant j'ai l'impression que cela montre juste que f est soit dérivable partout soit dérivable nul part, et je ne vois pas pourquoi le deuxième cas n'est pas possible.

[phyelec]

je n'aurais pas écris f'(x)=f'(1)/x mais plutôt ceci:



donc

[phyelec]

j'ai écris :"je n'aurais pas écris f'(x)=f'(1)/x mais plutôt ceci:" quoique avec f'(x)=af'(ax) si x=1 on a bien f'(a)=f'(1)/a pour tout à appartenant à R+*.

[phyelec]

pour la fonction f est dérivable seulement si f'(1) existe et donc si :

ou C est une constante.

On cherche une fonction f avec la propriété f(ab)=f(a)+f(b) . Je ne vois pas ce que l'on peut dire de plus.

[Napoléon]

On a montré que f (solution de l'équation fonctionnelle) est dérivable ssi f'(1) existe. Mais une fonction solution de l'équation est dérivable dès lors qu'elle est continue et c'est cela que j'aimerais montrer. C'est à dire que j'aimerais montrer qu'elle est dérivable sans avoir à supposer qu'elle est dérivable en 1 point.

[Ben314]

Salut,
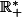
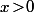
Comme est continue, existe et est dérivable sur et, pour tout , on a
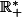
C'est à dire ce qui prouve que est dérivable sur vu que l'est.

[Napoléon]

Trop bien, merci beaucoup !

[phyelec]

oui trop bien Ben314.