Equation fonctionelle

par **polymathematic** » 22 Aoû 2006, 15:25

bonjour
voila le problem
je cherche a determiner les fonctions continues derivables sur

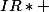
qui verifie

pour tout

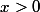
merci

PS:source du probleme [url=http://]www.maths-forum.com/showthread.php?t=17328&page=6&pp=10[/url]

par **aviateurpilot** » 22 Aoû 2006, 15:28

, k de IR

sont des solutions.
je vais essayer de montrer qu'il sont les seules
ou bien trouver des autre solution :++:

tu as un petit probleme dans le lien que tu as donné
http://www.maths-forum.com/showthread.php?t=17328&page=6&pp=10

par **polymathematic** » 22 Aoû 2006, 15:31

ok daccord
si ca marche ca vas avancer un peu le problem
sortez vos armes :arme:

par **polymathematic** » 22 Aoû 2006, 15:45

en fete il y a ca en plus

par **ayanis** » 22 Aoû 2006, 16:04

La fonction identiquement nulle est seule solution je pense, parce que abs(lnx) n'est pas dérivable en x=1.

par **polymathematic** » 22 Aoû 2006, 16:11

si la fonction nul est la seul solution ca serais cool

par **aviateurpilot** » 22 Aoû 2006, 16:22

supposons alors que la fonction nul est la seule solution,
tu va faire quoi dans ce cas? :++:

par **polymathematic** » 22 Aoû 2006, 16:29

ds ce cas j'arais h(x)=0 pour tt x
et apres ca donneF(x+1)=(1+1/x²)F(x)=F(x)+F(1/x) (Fdefin au problem F(x+1)=F(x)+F(1/x))
en suite F(1/x)=1/x²F(x) sauf erreur de ma part

par **aviateurpilot** » 22 Aoû 2006, 16:37

supposons que la seule solution de H(x)=H(1/x) est H(x)=0 (*)

tu as trouvé que F(1/x)=1/x²F(x)
on pose G(x)=F(x)/x
on a G(1/x)=xF(1/x)=F(x)/x=G(x)
doc d'apres (*) G(x)=0
donc F(x)=0

si on veux resoudre tt le probleme on ne doit que montrer (*)

par **nyafai** » 22 Aoû 2006, 16:40

salut
je viens de réfléchir un peu au problème et à priori voila une solution (peut-être fausse parce que ca me paraît bizarre...)

Analyse :soit f une telle fonction, on a pour tout x : f '(x)=-1/x²*f '(1/x) et
f '(1)=-f '(1) d'où f '(1)=0

synthèse : Soit g une fonction quelconque définie sur [1,+00[, continue et dérivable sur cet intervalle avec g(1)=0 et g '(1)=0 (dérivée à droite en 1). Il existe une infinité de telles fonctions.

soit f la fonction définie sur R+* par : pour x>=1 :f(x)=g(x)
pour x entre 0 et 1, f(x)= g(1/x)

On montre facilement que cette fonction vérifie bien f(x)=f(1/x)
elle est bien continue sur R+* et dérivable sur ]0,1[ et ]1,+00[ (découle de la continuité et dérivabilité de x->1/x sur ces intervalles)
le seul problème est la dérivabilité en 1 et en fait il se résout en calculant indé pendamment les limites de f(x)/(x-1) à droite et à gauche de 1

et donc toutes ces fonctions conviennent

par exemple: f(x)=(x-1)² sur [1,+00[ et f(x)=(1/x-1)² sur ]0,1] convient

à plus

par **aviateurpilot** » 22 Aoû 2006, 16:40

nyafai ,F n'ai pas forcement derivable

F(1/x)=1/x²F(x)
on pose G(x)=F(x)/x
on a G(1/x)=xF(1/x)=F(x)/x=G(x)
don G(x)=G(1/x)

par **nyafai** » 22 Aoû 2006, 16:54

ben si elle est dérivable partout à part en 1 puis que je définis g comme dérivablesur [1,+00[.

le problème est en 1 mais il se résout comme ça:
on sait que lim g(x)/x-1 en 1+ est nulle (g'(1)=0).

calculons lim f(x)/x-1 à gauche et à droite de 1 :

à droite : lim f(x)/x-1=lim g(x)/x-1=g'(1)=0

à gauche :lim f(x)/x-1=lim g(1/x)/x-1 =lim(changement de variable X=1/x, limite pour X->1+) de g(X)/(1/X-1)=X*g(X)/(1-X)=g'(1) =0

donc f est bien dérivable en 1

par **alben** » 22 Aoû 2006, 16:56

Bonsoir,

On peut effectivement trouver autant de fonctions f que l'on veut qui satisfassent ta relation.
Il suffit de choisir g continue et dérivable en R* et de poser f(x)=g(x)+g(1/x)
g peut être un polynome, un sinus, une exponentielle, et bien d'autre chose encore.
On pourrait également définir f par f(x)= g(x).g(1/x) ou bien racine[g(x)²+g²(1/x)] etc...
Je crois que, malheureusement, le passage par l'intégration ne résoudra pas le problème :triste:

par **ayanis** » 22 Aoû 2006, 17:00

nyafai a écrit:par exemple: f(x)=(x-1)² sur [1,+00[ et f(x)=(1/x-1)² sur ]0,1] convient

sauf que 1/(x-1)² vaut plus l'infini en 1, ca ne risque donc pas d'etre continu...

En effet, si dans un sens ta fonction est nulle, son inverse ne peut pas être nulle au même point... Ces solutions ne conviennent donc pas.

par **nyafai** » 22 Aoû 2006, 17:02

je ne parle pas de 1/(x-1)² mais de ((1/x)-1)² (=g(1/x))

par **ayanis** » 22 Aoû 2006, 17:05

Autant pour moi... suis vraiment fatiguée moi...
Désolée

par **nyafai** » 22 Aoû 2006, 17:06

pas de problème :++:

par **quinto** » 22 Aoû 2006, 17:24

ayanis a écrit:La fonction identiquement nulle est seule solution je pense, parce que abs(lnx) n'est pas dérivable en x=1.

Effectivement, mais on peut conserver l'idée.
Ici on a choisi une fonction paire, |.|, de sorte à oter le signe négatif. On s'est rendu compte que ca "cassait" la dérivabilité de notre fonction.
Aucun problème, il suffit de choisir une autre fonction paire et dérivable.
Un exemple est le suivant:
f(x)=kcos(k'log(x))

a+

par **buzard** » 22 Aoû 2006, 17:31

si tu ne considère que le'equation fonctionnelle f(x)=f(1/x)

les solutions sont toutes de la forme h(x)+h(1/x), h quelconque.

il ne te reste plus qu'à conclure avec la dérivabilité.

par **quinto** » 22 Aoû 2006, 17:31

En fait, il y'a une autre classe de fonctions intéressantes et qui permettent de résoudre notre problème:
Soit S(x,y) définie par une fonction S telle que S(x,y)=S(y,x)
Il suffit de poser f(x)=S(x,1/x).

Une telle fonction S est facile à trouver, par exemple on peut prendre S(x,y)=x+y.

Equation fonctionelle

equation fonctionelle

Qui est en ligne