Equation fonctionelle avec polynômes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 18 Juin 2008, 15:31
par Aspx » 18 Juin 2008, 15:31
Bonjour,
Je suis actuellement sur l'exercice suivant :
Déterminer tous les
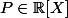
tels que
=P(X))
J'ai essayé de m'intéresser aux racines éventuelles de

. On voit facilement que si

est racine de

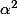
aussi puis à l'aide d'une application et du fait que le degré de

est fini on montre que toute racine est d'ordre fini, ce qui implique qu'elle est de module 1. Si je ne me trompe pas, j'en suis là pour l'instant. Ensuite la factorisation de

à l'aide de ses racines de module 1 ne me fait pas spécialement avancer et c'est ça mon problème.
Des idées pour continuer ?
Merci d'avance !
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 18 Juin 2008, 15:48
par Aspx » 18 Juin 2008, 15:48
Excuse moi je me suis trompé pour l'équation ! C'est
[CENTER]
=P(X-1)P(X))
[/CENTER]
:marteau:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 18 Juin 2008, 16:12
par lapras » 18 Juin 2008, 16:12
salut
Tu cherches les

?
ou on inclut les complexes ?
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 18 Juin 2008, 16:16
par Aspx » 18 Juin 2008, 16:16
Je cherche pas des fonctions mais des polynômes (dans
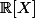
)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 18 Juin 2008, 16:19
par lapras » 18 Juin 2008, 16:19
Mais
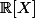
signifie que ses coeff. sont réels, mais le polynôme a bien un ensemble de définition, non ? (je ne connais pas beaucoup ce chapitre)
-
SimonB
 par SimonB » 18 Juin 2008, 17:08
par SimonB » 18 Juin 2008, 17:08
lapras a écrit:Mais
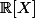
signifie que ses coeff. sont réels, mais le polynôme a bien un ensemble de définition, non ? (je ne connais pas beaucoup ce chapitre)
Non, un polynôme n'est pas une fonction. On peut parler de fonction polynomiale mais ça n'est pas formellement la même chose.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 18 Juin 2008, 17:26
par lapras » 18 Juin 2008, 17:26
Ok quelle est la différence ? (désolé de pourrir le topic...)
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 18 Juin 2008, 17:44
par Aspx » 18 Juin 2008, 17:44
La différence c'est qu'un polynôme est un ensemble de suites que l'on munit de l'addition et du produit bien connu, il n'y a pas d'ensemble de définition.
Plus précisément si

est un anneau commutatif on note

l'ensemble des suites presque nulles d'éléments de

.
On pose ensuite
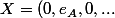)
etc...
On appelle polynôme à coefficient dans

un élément de

-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 18 Juin 2008, 19:12
par ThSQ » 18 Juin 2008, 19:12
Aspx a écrit:Excuse moi je me suis trompé pour l'équation ! C'est
[CENTER]
=P(X-1)P(X))
[/CENTER]
:marteau:
On élimine les sol avec d°P (1+x)², comme il y a un nombre fini de zéros ils sont à prendre dans {-1, j, j² }.
-1 marche pas (voir avec X=0).
P(X) = (X²+X+1)^n + P=0 sols

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 18 Juin 2008, 19:25
par leon1789 » 18 Juin 2008, 19:25
lapras a écrit:Ok quelle est la différence ? (désolé de pourrir le topic...)
Sur les anneaux contenant Z, on peut dire qu'il n'y a pas de différence.
Mais dans d'autres circonstances, ça peut se gatter : sur Z/pZ , le polynôme X^p-X est un polynôme non nul de degré p, mais le fonction polynomiale x -> x^p-x est la fonction nulle.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 18 Juin 2008, 19:32
par leon1789 » 18 Juin 2008, 19:32
Aspx a écrit:La différence c'est que l'
anneau des polynômes est un ensemble de suites que l'on munit de
l'addition et du produit bien connu, il n'y a pas d'ensemble de définition.
Plus précisément si

est un anneau commutatif on note

l'ensemble des suites presque nulles d'éléments de

.
On pose ensuite
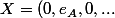)
etc...
L'addition est alors l'addition terme à terme (
addition naturelle si je peux dire), mais
la multiplication n'est absolument pas intuitive avec cette présentation ! La multiplication naturelle serait terme à terme, mais là, ce n'est pas l'anneau des polynômes...
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 18 Juin 2008, 19:39
par Aspx » 18 Juin 2008, 19:39
ThSQ a écrit:On élimine les sol avec d°P (1+x)², comme il y a un nombre fini de zéros ils sont à prendre dans {-1, j, j² }.
-1 marche pas (voir avec X=0).
P(X) = (X²+X+1)^n + P=0 sols
C'est parfait merci beaucoup pour l'idée de la stabilité par
^2)
:we: !
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 18 Juin 2008, 19:46
par Aspx » 18 Juin 2008, 19:46
leon1789 a écrit:L'addition est alors l'addition terme à terme (addition naturelle si je peux dire), mais la multiplication n'est absolument pas intuitive avec cette présentation ! La multiplication naturelle serait terme à terme, mais là, ce n'est pas l'anneau des polynômes...
Je voulais ne voulais pas dire intuitive au sens des suites mais au sens des fonctions polynomiales. Mais bon tant qu'à être précis :
@lapras : L'addition est définie terme à terme et pour la multiplication si
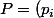_{i\in\mathbb{N}},Q=(q_i)_{i\in\mathbb{N}} \in \mathbb{R}[X])
on définit
[CENTER]
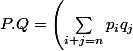_{n\in\mathbb{N}})
[/CENTER]
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
est un anneau commutatif on note
l'ensemble des suites presque nulles d'éléments de
.
etc...