Bonjour,
J'ai l'équation diff suivante :
y'+2y=e^(-2t)
Pour la solution générale lorsque l'équation est homogène ça ne pose pas de soucis , seulement pour la solution particulière j'ai ça :
e^(-2t) est du type f(t) =Ae^(-2t)
soit f'(t)= -2Ae^(-2t)
Nous avons donc à poser : -2Ae^(-2t) + 2*(Ae^(-2t)) = e^(-2t)
Soit : -2A +2 A = 1 => seulement là ça n'est pas possible .
Pouvez m'aider s'il vous plait,
Merci par avance,
Equation différentielle sans solution??
5 messages
- Page 1 sur 1
Re: Equation différentielle sans solution??
salut
mais que fais-tu pour avoir une solution particulière ?
mais que fais-tu pour avoir une solution particulière ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Equation différentielle sans solution??
L'équa diff a forcément une solution
Maintenant c'est possible qu'une solution particulière n'est pas du type Aexp(-2t)
Ce que tu peux faire c'est augmenter le degré
 = (At+B)e^{-2t})
Alors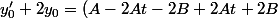e^{-2t} = e^{-2t})
Maintenant c'est possible qu'une solution particulière n'est pas du type Aexp(-2t)
Ce que tu peux faire c'est augmenter le degré
Alors
Re: Equation différentielle sans solution??
Nickel merci beaucoup à tous ,je tâcherai de me rappeler de cette astuce pour l'examen !
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
