Equation demi tangente.
14 messages
- Page 1 sur 1
Equation demi tangente.
salut à tous,
Voilà le titre résume tout. Comment trouver les équations de demi tangente à un point de rebrousement ou point anguleux?
Merci d'avance !
Voilà le titre résume tout. Comment trouver les équations de demi tangente à un point de rebrousement ou point anguleux?
Merci d'avance !
En effet dans le cas d'une fonction f(x)=|ax²+b+c|
la fonction va s'annuler en x1 = [-b-;)(b²-4ac)]/(2a) et x2 = [-b+;)(b²-4ac)]/(2a) si delta positif.
si on utilise la formule y=f'(a)(x-a)+f(a) on obtiendra la même équation pour les deux demi-tangentes en x1 et x2 (si ils existent), bien que l'une soit la symétrique de l'autre par l'axe des abscisses (Ox). Suffit-il alors d'inverser le signe de la première équation pour trouver l'équation de l'autre demi-tangentes?
la fonction va s'annuler en x1 = [-b-;)(b²-4ac)]/(2a) et x2 = [-b+;)(b²-4ac)]/(2a) si delta positif.
si on utilise la formule y=f'(a)(x-a)+f(a) on obtiendra la même équation pour les deux demi-tangentes en x1 et x2 (si ils existent), bien que l'une soit la symétrique de l'autre par l'axe des abscisses (Ox). Suffit-il alors d'inverser le signe de la première équation pour trouver l'équation de l'autre demi-tangentes?
bitonio a écrit:euh c'est clairement pas dérivable en les racines ton truc...
regarde |x| en 0 et donne moi une tangente
Effectivement, mais il y a deux demi-tangentes d'équation, y=-x et y=x pour la fonction f(x) = |x| en 0. Comment prouver que la fonction f(x) = |x²-3x+2| par exemple a pour demi équation en 1 : y=-x+1 a gauche et y=x-1 à droite (je en suis pas sûre de ce que j'avance...) !
Lol (en retard) Fahr 451... j'avais pas compris...
Bon, tu supposes x n'appartient pas à l'intervale des racines
donc tu as ta fonction qui est positive à l'interieur de la valeur absolue. Tu peux donc l'enlever.
Tu dérives, tu obtiens ta fonction dérivée
Tu fais pareil à l'intérieur, tu as une autre dérivée. (la mm avec un -)
Ta dérivée est continue sur R privée des racines, donc continue à gauche et à droite de chaque racine.
Donc tu conclues par passage à la limite en utilisant le théorème de prolongement C^1
Voila, sauf erreur :ptdr:
donc tu as ta fonction qui est positive à l'interieur de la valeur absolue. Tu peux donc l'enlever.
Tu dérives, tu obtiens ta fonction dérivée
Tu fais pareil à l'intérieur, tu as une autre dérivée. (la mm avec un -)
Ta dérivée est continue sur R privée des racines, donc continue à gauche et à droite de chaque racine.
Donc tu conclues par passage à la limite en utilisant le théorème de prolongement C^1
Voila, sauf erreur :ptdr:
bitonio a écrit:Bon, tu supposes x n'appartient pas à l'intervale des racines
donc tu as ta fonction qui est positive à l'interieur de la valeur absolue. Tu peux donc l'enlever.
Tu dérives, tu obtiens ta fonction dérivée
Tu fais pareil à l'intérieur, tu as une autre dérivée. (la mm avec un -)
Ta dérivée est continue sur R privée des racines, donc continue à gauche et à droite de chaque racine.
Donc tu conclues par passage à la limite en utilisant le théorème de prolongement C^1
Tout ce que tu dis j'ai réussit à faire sauf le théoreme du prolongement que je ne connais pas. Mais ma question n'est pas ceci. C'est comment trouver l'équation de la demi tangente en 1- et en 1+ de même en 2- et 2+ pour la fonction dont j'ai donné l'exmple !
f(x) =x²-3x+2, on considère donc x à l'extérieur des racines.
f'(x)=2x-3.
donc en faisant tendre f'(x) vers 1- on trouve f'(1)=-1
donc tu as la valeur de ton nombre dérivé, donc la tengante.
maintenant, si x appartient à ]1;2[, f'(x)=-2x+3, donc f'(1+)=1
etc...
Le théroème de prolongement C1:
soit une fonction C1 sur [a;b[
si limf'(x) existe quand x=>b, alors f'(b) existe et ta fonction est C1 sur [a;b]. C'est ce qui premet de justifier l'existence de la dérivée à gauche et à droite ici
Bonne chance
f'(x)=2x-3.
donc en faisant tendre f'(x) vers 1- on trouve f'(1)=-1
donc tu as la valeur de ton nombre dérivé, donc la tengante.
maintenant, si x appartient à ]1;2[, f'(x)=-2x+3, donc f'(1+)=1
etc...
Le théroème de prolongement C1:
soit une fonction C1 sur [a;b[
si limf'(x) existe quand x=>b, alors f'(b) existe et ta fonction est C1 sur [a;b]. C'est ce qui premet de justifier l'existence de la dérivée à gauche et à droite ici
Bonne chance
En effet en utilisant la formule y=f'(a)(x-a)+f(a) tu trouve la demi-tangente en 1 et 2 correspondant à la tangente en ces points pour la courbe C de la fonction f(x) = |x²-3x+2|. Mais pour trouver la demi-tangente en 1 et 2 correspondant à la partie de la courbe correspondant à |x²-3x+2|=-x²+3x-2 il faut multiplier les deux équations trouvé par -1 !
Ainsi en 1 on obtiens l'équation de la demi tangente situé à gauche y=-x+1 et la demi tangente à droite admet l'équation y=x-1 ! Mais voilà comment justifier.
Enfin bref. J'ai la reponse, mais j'ai du mal à justifier, j'attendrai la correction § merci beaucoup :we:
Ainsi en 1 on obtiens l'équation de la demi tangente situé à gauche y=-x+1 et la demi tangente à droite admet l'équation y=x-1 ! Mais voilà comment justifier.
Enfin bref. J'ai la reponse, mais j'ai du mal à justifier, j'attendrai la correction § merci beaucoup :we:
lis mon message je t'ai justifié la différence de signe entre les deux!
Je te réexplique:
Soit x ]-oo;1[U]2;+oo[
]-oo;1[U]2;+oo[
f(x)=x^2-3x+1
f'(x)=2x-3
Donc
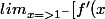=-1 ]) , donc par le théorème de prolongement
, donc par le théorème de prolongement  tu as
tu as ) qui existe et qui vaut -1
qui existe et qui vaut -1
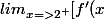=1]) , donc par le théorème de prolongement
, donc par le théorème de prolongement  tu as
tu as ) qui existe et qui vaut 1
qui existe et qui vaut 1
Sinon, f'(x)=3-2x
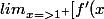=1]) , donc par le théorème de prolongement
, donc par le théorème de prolongement  tu as
tu as ) qui existe et qui vaut 1
qui existe et qui vaut 1
=-1]) , donc par le théorème de prolongement
, donc par le théorème de prolongement  tu as
tu as ) qui existe et qui vaut -1
qui existe et qui vaut -1
voilou
Je te réexplique:
Soit x
f(x)=x^2-3x+1
f'(x)=2x-3
Donc
Sinon, f'(x)=3-2x
voilou
bitonio a écrit:f(x) =x²-3x+2, on considère donc x à l'extérieur des racines.
f'(x)=2x-3.
donc en faisant tendre f'(x) vers 1- on trouve f'(1)=-1
donc tu as la valeur de ton nombre dérivé, donc la tengante.
maintenant, si x appartient à ]1;2[, f'(x)=-2x+3, donc f'(1+)=1
etc...
Le théroème de prolongement C1:
soit une fonction C1 sur [a;b[
si limf'(x) existe quand x=>b, alors f'(b) existe et ta fonction est C1 sur [a;b]. C'est ce qui premet de justifier l'existence de la dérivée à gauche et à droite ici
Bonne chance
Merci tu as répondu à ma recherche de la justification parfaite ^^
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
